|
 |
|
|
 #1
Nell'esercizio 6 del testo Teoria dei Sistemi: Esercizi e Applicazioni,
(modello matematico di un satellite) svolto durante le
esercitazioni e sul libro ho notato che non sono state considerate la
rivoluzione terrestre né gli effetti relativistici.
Soprattutto m'interessa l'omissione della rivoluzione. (Daniele Cremonini) #1
Nell'esercizio 6 del testo Teoria dei Sistemi: Esercizi e Applicazioni,
(modello matematico di un satellite) svolto durante le
esercitazioni e sul libro ho notato che non sono state considerate la
rivoluzione terrestre né gli effetti relativistici.
Soprattutto m'interessa l'omissione della rivoluzione. (Daniele Cremonini)
 L'esercizio 6 tratta il classico problema dei "due corpi"; la rotazione
attorno al proprio asse del corpo (terra) attorno al quale il secondo
(satellite) orbita non è stata introdotta perché non rilevante
rispetto alle finalità dell'esercizio. Lo stesso può essere
ripetuto per la correzione relativistica. Nelle applicazioni pratiche tali
fattori devono venire introdotti; le prestazioni del sistema di navigazione
satellitare GPS, ad esempio, risulterebbero decisamente inferiori se non
si considerasse la correzione prevista dalla teoria della relatività.
L'esercizio 6 tratta il classico problema dei "due corpi"; la rotazione
attorno al proprio asse del corpo (terra) attorno al quale il secondo
(satellite) orbita non è stata introdotta perché non rilevante
rispetto alle finalità dell'esercizio. Lo stesso può essere
ripetuto per la correzione relativistica. Nelle applicazioni pratiche tali
fattori devono venire introdotti; le prestazioni del sistema di navigazione
satellitare GPS, ad esempio, risulterebbero decisamente inferiori se non
si considerasse la correzione prevista dalla teoria della relatività.
 #2
Come bisogna dimensionare la frequenza di campionamento una volta noto il
tempo di salita? (Daniele Cremonini) #2
Come bisogna dimensionare la frequenza di campionamento una volta noto il
tempo di salita? (Daniele Cremonini)
 La frequenza minima di campionamento va determinata, con il teorema
di Shannon, in base alla frequenza massima presente nei segnali che si
intende campionare o, perlomeno, della componente a frequenza massima
del segnale che si intende riprodurre correttamente. Il "tempo di salita"
fornisce una indicazione di massima sulla banda passante di un sistema
dinamico lineare e può quindi venire utilizzato per un dimensionamento,
pure di massima, del campionamento da effettuare sull'uscita di tale
sistema. Regole empiriche talvolta utilizzate consistono nell'adottare
un tempo di campionamento pari ad un decimo del tempo di salita o di
quello di assestamento.
La frequenza minima di campionamento va determinata, con il teorema
di Shannon, in base alla frequenza massima presente nei segnali che si
intende campionare o, perlomeno, della componente a frequenza massima
del segnale che si intende riprodurre correttamente. Il "tempo di salita"
fornisce una indicazione di massima sulla banda passante di un sistema
dinamico lineare e può quindi venire utilizzato per un dimensionamento,
pure di massima, del campionamento da effettuare sull'uscita di tale
sistema. Regole empiriche talvolta utilizzate consistono nell'adottare
un tempo di campionamento pari ad un decimo del tempo di salita o di
quello di assestamento.
 #3
Oltre al tempo di salita cosa si può osservare per stabilire le
costanti di tempo? (Daniele Cremonini) #3
Oltre al tempo di salita cosa si può osservare per stabilire le
costanti di tempo? (Daniele Cremonini)
 Le costanti di tempo di un sistema lineare sono deducibili dai poli dello
stesso, quindi dalla conoscenza della funzione di trasferimento.
La funzione di trasferimento determina anche la risposta frequenziale
e può quindi venire utilizzata per determinare, in maniera non
empirica, un campionamento idoneo sull'uscita. Si noti come l'eventuale
presenza nel segnale di ingresso di frequenze superiori a quelle
riproducibili dal sistema non giochi (nei sistemi lineari) alcun
ruolo nella determinazione del tempo di campionamento.
Le costanti di tempo di un sistema lineare sono deducibili dai poli dello
stesso, quindi dalla conoscenza della funzione di trasferimento.
La funzione di trasferimento determina anche la risposta frequenziale
e può quindi venire utilizzata per determinare, in maniera non
empirica, un campionamento idoneo sull'uscita. Si noti come l'eventuale
presenza nel segnale di ingresso di frequenze superiori a quelle
riproducibili dal sistema non giochi (nei sistemi lineari) alcun
ruolo nella determinazione del tempo di campionamento.
 #4
Nell'undicesimo test del capitolo sui sistemi lineari non stazionari
del testo Teoria dei Sistemi: Test commentati e risolti,
si afferma che in un sistema lineare non stazionario continuo gli elementi
di C(t) sono funzioni continue a tratti.
Mi sembra di aver capito che in un sistema non stazionario la variabilità
degli elementi delle matrici caratteristiche rappresenti la variazione nel
tempo di parametri fisici del sistema; come è possibile che siano
funzioni continue a tratti? Esiste un esempio ? (Paolo Bastia) #4
Nell'undicesimo test del capitolo sui sistemi lineari non stazionari
del testo Teoria dei Sistemi: Test commentati e risolti,
si afferma che in un sistema lineare non stazionario continuo gli elementi
di C(t) sono funzioni continue a tratti.
Mi sembra di aver capito che in un sistema non stazionario la variabilità
degli elementi delle matrici caratteristiche rappresenti la variazione nel
tempo di parametri fisici del sistema; come è possibile che siano
funzioni continue a tratti? Esiste un esempio ? (Paolo Bastia)
 Discontinuità nei parametri che definiscono il modello di un
sistema possono essere causate da azioni di controllo sul sistema
stesso e sono abbastanza frequenti nella pratica. Un esempio
realistico è descritto nell'esercizio 9 del testo Teoria
dei Sistemi: Esercizi e Applicazioni (carrello
a trazione elettrica), dove la frenatura determina la
commutazione tra due modelli. In tale caso è possibile
descrivere il sistema sia con un modello stazionario non lineare
che include tra i propri ingressi l'azione di controllo, sia con
un modello lineare non stazionario (come viene fatto nell'esercizio
indicato che considera i due modelli relativi alle diverse condizioni
operative).
Discontinuità nei parametri che definiscono il modello di un
sistema possono essere causate da azioni di controllo sul sistema
stesso e sono abbastanza frequenti nella pratica. Un esempio
realistico è descritto nell'esercizio 9 del testo Teoria
dei Sistemi: Esercizi e Applicazioni (carrello
a trazione elettrica), dove la frenatura determina la
commutazione tra due modelli. In tale caso è possibile
descrivere il sistema sia con un modello stazionario non lineare
che include tra i propri ingressi l'azione di controllo, sia con
un modello lineare non stazionario (come viene fatto nell'esercizio
indicato che considera i due modelli relativi alle diverse condizioni
operative).
 #5
Non ho ben capito perché il sottospazio di raggiungibilità
di un sistema lineare e stazionario sia il più piccolo invariante
rispetto ad A contenente l'immagine di B.
(Pierpaolo Libanori) #5
Non ho ben capito perché il sottospazio di raggiungibilità
di un sistema lineare e stazionario sia il più piccolo invariante
rispetto ad A contenente l'immagine di B.
(Pierpaolo Libanori)
 Per il sottospazio di raggiungibilità abbiamo ricavato, sia per i
sistemi continui che per quelli discreti, l'espressione
im[B AB ... A(n-1)B].
L'invarianza rispetto ad A è quindi una conseguenza immediata
del teorema di Cayley-Hamilton; l'espressione precedente evidenzia inoltre
come l'immagine di B risulti contenuta in tale sottospazio.
Consideriamo adesso un sottospazio generico, Z, invariante rispetto
ad A e contenente l'immagine di B; ne segue che (i vettori
costituiti dal)le colonne di B appartengono a Z.
Per l'ipotesi di invarianza di Z rispetto ad A anche le colonne
di AB ... A(n-1)B apparterranno a Z;
quindi l'intero sottospazio di raggiungibilità è contenuto
in Z. Essendo però Z un qualunque sottospazio invariante
rispetto ad A e contenente l'immagine di B, ne segue che il
sottospazio di raggiungibilità è contenuto in ogni
sottospazio invariante rispetto ad A e contenente l'immagine di B.
È quindi il più piccolo sottospazio che goda di tale
proprietà.
Per il sottospazio di raggiungibilità abbiamo ricavato, sia per i
sistemi continui che per quelli discreti, l'espressione
im[B AB ... A(n-1)B].
L'invarianza rispetto ad A è quindi una conseguenza immediata
del teorema di Cayley-Hamilton; l'espressione precedente evidenzia inoltre
come l'immagine di B risulti contenuta in tale sottospazio.
Consideriamo adesso un sottospazio generico, Z, invariante rispetto
ad A e contenente l'immagine di B; ne segue che (i vettori
costituiti dal)le colonne di B appartengono a Z.
Per l'ipotesi di invarianza di Z rispetto ad A anche le colonne
di AB ... A(n-1)B apparterranno a Z;
quindi l'intero sottospazio di raggiungibilità è contenuto
in Z. Essendo però Z un qualunque sottospazio invariante
rispetto ad A e contenente l'immagine di B, ne segue che il
sottospazio di raggiungibilità è contenuto in ogni
sottospazio invariante rispetto ad A e contenente l'immagine di B.
È quindi il più piccolo sottospazio che goda di tale
proprietà.
 #6
Non mi è molto chiara la regola che lei ha esposto a lezione
riguardante la matrice P=[B AB....A(n-1)B]
relativa alla lineare dipendenza delle sue colonne. Non riesco inoltre a
capire l'importanza pratica di questa regola. (Stefano Lucente) #6
Non mi è molto chiara la regola che lei ha esposto a lezione
riguardante la matrice P=[B AB....A(n-1)B]
relativa alla lineare dipendenza delle sue colonne. Non riesco inoltre a
capire l'importanza pratica di questa regola. (Stefano Lucente)
 L'espressione della matrice di raggiungibilità che abbiamo ricavato
si presta a tre considerazioni di carattere pratico particolarmente utili
nel calcolo manuale non tanto e non solo di tale matrice ma, soprattutto,
del sottospazio di raggiungibilità generato dalle sue colonne.
La prima osservazione riguarda le sottomatrici AkB che
risulta vantaggioso calcolare premoltiplicando per A il blocco
precedente, evitando cioè il calcolo esplicito di Ak;
tale modo di procedere riduce
la mole di calcoli e la possibilità di errori. Le osservazioni
relative alla lineare dipendenza delle colonne riducono, egualmente,
i calcoli necessari alla determinazione di im(P). La prima osservazione
riguarda la lineare dipendenza di tutti i blocchi successivi alla prima
sottomatrice le cui colonne risultino tutte linearmente dipendenti dalle
precedenti; è ovvio l'uso di tale risultato: anziché
calcolare tutti i blocchi di P ed applicare l'algoritmo di Gram-Schmidt
alle colonne di tale matrice, si calcolerà un blocco alla volta
valutando la lineare dipendenza delle sue colonne dai vettori precedenti
sospendendo la procedura quando si incontra un blocco le cui colonne
siano tutte linearmente dipendenti dalle precedenti.
La seconda osservazione riguarda la lineare dipendenza di tutti i vettori
di posizione omologa nei blocchi successivi quando si osserva la lineare
dipendenza (da tutti i vettori precedenti) di un singolo vettore
all'interno di un blocco di P; l'uso pratico di tale proprietà,
del tutto simile al precedente, consente di ridurre al minimo
le operazioni necessarie al calcolo di una base del sottospazio di
raggiungibilità. Esempi numerici di applicazione di tali
regole sono riportati negli esercizi 1 (Raggiungibilità,
osservabilità e stabilità) e 2 (Scomposizione di Kalman,
forma minima) del testo Teoria dei Sistemi: Esercizi e Applicazioni.
L'espressione della matrice di raggiungibilità che abbiamo ricavato
si presta a tre considerazioni di carattere pratico particolarmente utili
nel calcolo manuale non tanto e non solo di tale matrice ma, soprattutto,
del sottospazio di raggiungibilità generato dalle sue colonne.
La prima osservazione riguarda le sottomatrici AkB che
risulta vantaggioso calcolare premoltiplicando per A il blocco
precedente, evitando cioè il calcolo esplicito di Ak;
tale modo di procedere riduce
la mole di calcoli e la possibilità di errori. Le osservazioni
relative alla lineare dipendenza delle colonne riducono, egualmente,
i calcoli necessari alla determinazione di im(P). La prima osservazione
riguarda la lineare dipendenza di tutti i blocchi successivi alla prima
sottomatrice le cui colonne risultino tutte linearmente dipendenti dalle
precedenti; è ovvio l'uso di tale risultato: anziché
calcolare tutti i blocchi di P ed applicare l'algoritmo di Gram-Schmidt
alle colonne di tale matrice, si calcolerà un blocco alla volta
valutando la lineare dipendenza delle sue colonne dai vettori precedenti
sospendendo la procedura quando si incontra un blocco le cui colonne
siano tutte linearmente dipendenti dalle precedenti.
La seconda osservazione riguarda la lineare dipendenza di tutti i vettori
di posizione omologa nei blocchi successivi quando si osserva la lineare
dipendenza (da tutti i vettori precedenti) di un singolo vettore
all'interno di un blocco di P; l'uso pratico di tale proprietà,
del tutto simile al precedente, consente di ridurre al minimo
le operazioni necessarie al calcolo di una base del sottospazio di
raggiungibilità. Esempi numerici di applicazione di tali
regole sono riportati negli esercizi 1 (Raggiungibilità,
osservabilità e stabilità) e 2 (Scomposizione di Kalman,
forma minima) del testo Teoria dei Sistemi: Esercizi e Applicazioni.
 #7
Perché è importante poter influire sulla prontezza della
stima di un osservatore dello stato? Con la locuzione "prontezza della stima"
intendo la velocità con cui la stima stessa tende ad eguagliare lo
stato effettivo del sistema. (Pierpaolo Libanori) #7
Perché è importante poter influire sulla prontezza della
stima di un osservatore dello stato? Con la locuzione "prontezza della stima"
intendo la velocità con cui la stima stessa tende ad eguagliare lo
stato effettivo del sistema. (Pierpaolo Libanori)
 L'osservatore dello stato è un sistema dinamico che, collegato
all'ingresso ed all'uscita di un sistema di cui si vuole osservare lo
stato, è soggetto ad una evoluzione che porta il suo stato a
coincidere, asintoticamente, con quello del sistema da osservare.
Una volta che tale coincidenza è stata acquisita,
gli stati dei due sistemi hanno la stessa evoluzione.
Lo stato iniziale dell'osservatore viene, in assenza di altre informazioni,
azzerato; l'errore di stima ha una evoluzione che, come si è visto,
dipende solo dalla matrice dinamica dell'osservatore stesso. Una elevata
prontezza riduce la durata di tale transitorio, rende cioè la
stima accurata dopo un tempo sufficientemente breve rispetto al momento
nel quale l'osservatore è stato collegato; tale vantaggio
è tuttavia bilanciato dalla maggior sensibilità
dell'osservatore rispetto ai disturbi inevitabilmente presenti sulle
misure degll'ingresso e dell'uscita del sistema da osservare. Nella
pratica la matrice dinamica dell'osservatore viene scelta in base ad
un compromesso tra prontezza e insensibilità ai disturbi.
L'osservatore dello stato è un sistema dinamico che, collegato
all'ingresso ed all'uscita di un sistema di cui si vuole osservare lo
stato, è soggetto ad una evoluzione che porta il suo stato a
coincidere, asintoticamente, con quello del sistema da osservare.
Una volta che tale coincidenza è stata acquisita,
gli stati dei due sistemi hanno la stessa evoluzione.
Lo stato iniziale dell'osservatore viene, in assenza di altre informazioni,
azzerato; l'errore di stima ha una evoluzione che, come si è visto,
dipende solo dalla matrice dinamica dell'osservatore stesso. Una elevata
prontezza riduce la durata di tale transitorio, rende cioè la
stima accurata dopo un tempo sufficientemente breve rispetto al momento
nel quale l'osservatore è stato collegato; tale vantaggio
è tuttavia bilanciato dalla maggior sensibilità
dell'osservatore rispetto ai disturbi inevitabilmente presenti sulle
misure degll'ingresso e dell'uscita del sistema da osservare. Nella
pratica la matrice dinamica dell'osservatore viene scelta in base ad
un compromesso tra prontezza e insensibilità ai disturbi.
 #8
Vorrei sapere che cosa è una matrice ciclica e che ruolo ha nella
raggiungibilità dei sistemi lineari e stazionari con un unico
ingresso. (Mirko Tedaldi) #8
Vorrei sapere che cosa è una matrice ciclica e che ruolo ha nella
raggiungibilità dei sistemi lineari e stazionari con un unico
ingresso. (Mirko Tedaldi)
 Una matrice A (n x n) può venire definita
ciclica quando consente di generare l'intero spazio mediante un
unico generatore; in altri termini quando esiste un vettore v
(n x 1) tale che la matrice [v Av ... A(n-1)v]
sia di
rango massimo. Un sistema dotato di un solo ingresso può risultare
completamente raggiungibile solo se la relativa matrice dinamica è
ciclica. Tale proprietà può venire espressa anche in altri
modi, ad esempio facendo riferimento alla forma di Jordan o al polinomio
minimo e a quello caratteristico della matrice (che risultano coincidenti
per le matrici cicliche). In una matrice non ciclica la dimensione
massima del sottospazio generato da un singolo generatore coincide con
il grado del polinomio minimo.
Una matrice A (n x n) può venire definita
ciclica quando consente di generare l'intero spazio mediante un
unico generatore; in altri termini quando esiste un vettore v
(n x 1) tale che la matrice [v Av ... A(n-1)v]
sia di
rango massimo. Un sistema dotato di un solo ingresso può risultare
completamente raggiungibile solo se la relativa matrice dinamica è
ciclica. Tale proprietà può venire espressa anche in altri
modi, ad esempio facendo riferimento alla forma di Jordan o al polinomio
minimo e a quello caratteristico della matrice (che risultano coincidenti
per le matrici cicliche). In una matrice non ciclica la dimensione
massima del sottospazio generato da un singolo generatore coincide con
il grado del polinomio minimo.
 #9
Non ho capito perché risulti completamente raggiungibile un
sistema dinamico la cui matrice dinamica sia in forma di Jordan ed
in cui le righe della matrice di distribuzione degli ingressi
corrispondenti all'ultima riga dei blocchi di Jordan associati allo
stesso autovalore siano linearmente indipendenti. (Gabriele Tinti) #9
Non ho capito perché risulti completamente raggiungibile un
sistema dinamico la cui matrice dinamica sia in forma di Jordan ed
in cui le righe della matrice di distribuzione degli ingressi
corrispondenti all'ultima riga dei blocchi di Jordan associati allo
stesso autovalore siano linearmente indipendenti. (Gabriele Tinti)
 Il Teorema cui fa riferimento la proprietà descritta (e quella
duale relativa alla osservabilità) è basato sulle
proprietà dei sottospazi generati da una matrice non ciclica,
quindi con più blocchi di Jordan associati allo stesso
autovalore. Per tali matrici (si veda anche la domanda 8) un solo
generatore non può generare l'intero spazio. Una dimostrazione
del teorema in oggetto è riportata, sul testo Teoria dei
Sistemi e del Controllo di G. Marro.
Il Teorema cui fa riferimento la proprietà descritta (e quella
duale relativa alla osservabilità) è basato sulle
proprietà dei sottospazi generati da una matrice non ciclica,
quindi con più blocchi di Jordan associati allo stesso
autovalore. Per tali matrici (si veda anche la domanda 8) un solo
generatore non può generare l'intero spazio. Una dimostrazione
del teorema in oggetto è riportata, sul testo Teoria dei
Sistemi e del Controllo di G. Marro.
 #10
Sono corrette, per i sistemi lineari e stazionari, le seguenti
implicazioni? #10
Sono corrette, per i sistemi lineari e stazionari, le seguenti
implicazioni?
1 - controllabilità
2 - raggiungibilità
3 - completa controllabilità
4 - completa raggiungibilità
5 - osservabilità
6 - ricostruibilità
7 - diagnosticabilità
8 - incasellabilità
9 - completa osservabilità
10 - completa ricostruibilità
5=>6, 7=>8, 9=>10, 9=>7=>5 quindi 9=>6 e 9=>8, 10=>8=>6.
(Daniele Cremonini)
 Sì. Considerando classi particolari di sistemi dinamici è
possibile, come sappiamo, introdurre ulteriori implicazioni.
Sì. Considerando classi particolari di sistemi dinamici è
possibile, come sappiamo, introdurre ulteriori implicazioni.
 #11
Nella trattazione dei sistemi lineari non stazionari abbiamo enunciato
la proprietà secondo la quale gli elementi della matrice di
transizione sono funzioni continue del tempo.
Possiamo quindi dire che il moto libero è rappresentato da una
funzione continua perchè combinazione lineare di colonne della
matrice di transizione?.
E per quanto riguarda il moto totale (libero + forzato)?
Inoltre, a cosa sono dovute le discontinuità sulla velocità
di variazione di stato? (Luca Roffia) #11
Nella trattazione dei sistemi lineari non stazionari abbiamo enunciato
la proprietà secondo la quale gli elementi della matrice di
transizione sono funzioni continue del tempo.
Possiamo quindi dire che il moto libero è rappresentato da una
funzione continua perchè combinazione lineare di colonne della
matrice di transizione?.
E per quanto riguarda il moto totale (libero + forzato)?
Inoltre, a cosa sono dovute le discontinuità sulla velocità
di variazione di stato? (Luca Roffia)
 L'interpretazione relativa al moto libero è corretta. Per quanto
riguarda il moto forzato è sufficiente osservare come la funzione di
ingresso sia presente solo sotto il segno di integrale; eventuali
discontinuità dell'ingresso non danno quindi luogo a
discontinuità del moto. Le discontinuità possibili sulla
velocità di variazione dello stato sono dovute all'azione diretta
(algebrica) dell'ingresso su tale velocità (termine B(t)u(t)
nell'equazione di stato).
L'interpretazione relativa al moto libero è corretta. Per quanto
riguarda il moto forzato è sufficiente osservare come la funzione di
ingresso sia presente solo sotto il segno di integrale; eventuali
discontinuità dell'ingresso non danno quindi luogo a
discontinuità del moto. Le discontinuità possibili sulla
velocità di variazione dello stato sono dovute all'azione diretta
(algebrica) dell'ingresso su tale velocità (termine B(t)u(t)
nell'equazione di stato).
 #12
Nella trattazione della controllabilità ed osservabilità dei
sistemi dinamici lineari, facendo riferimento alla forma di Jordan, sono
stati ricavati il numero minimo di ingressi compatibili con la completa
raggiungibilità ed il numero minimo di uscite compatibili con la
completa osservabiltà.
Non ho ben chiaro come sono stati ricavati ed inoltre il legame che sussiste
fra essi. (Luca Roffia) #12
Nella trattazione della controllabilità ed osservabilità dei
sistemi dinamici lineari, facendo riferimento alla forma di Jordan, sono
stati ricavati il numero minimo di ingressi compatibili con la completa
raggiungibilità ed il numero minimo di uscite compatibili con la
completa osservabiltà.
Non ho ben chiaro come sono stati ricavati ed inoltre il legame che sussiste
fra essi. (Luca Roffia)
 Il risultato cui lei fa riferimento non è stato ricavato
ma solo enunciato (si veda anche la risposta 9). Il numero minimo di
ingressi compatibile con la completa raggiungibilità coincide
con quello di uscite compatibile con la completa osservabilità
essendo entrambi pari al numero massimo di blocchi di Jordan
associati allo stesso autovalore della matrice dinamica del sistema
in base al Teorema che abbiamo visto durante il corso.
Il risultato cui lei fa riferimento non è stato ricavato
ma solo enunciato (si veda anche la risposta 9). Il numero minimo di
ingressi compatibile con la completa raggiungibilità coincide
con quello di uscite compatibile con la completa osservabilità
essendo entrambi pari al numero massimo di blocchi di Jordan
associati allo stesso autovalore della matrice dinamica del sistema
in base al Teorema che abbiamo visto durante il corso.
 #13
In che caso, nei sistemi lineari non stazionari continui, il sottospazio
R+ risulta uguale al sottospazio R-?
E se il sistema è discreto, come possiamo dire che
dim R+ è minore o uguale a dim R-?
È forse dovuto al fatto che, in questo caso,
la matrice di transizione può essere singolare? (Luca Roffia) #13
In che caso, nei sistemi lineari non stazionari continui, il sottospazio
R+ risulta uguale al sottospazio R-?
E se il sistema è discreto, come possiamo dire che
dim R+ è minore o uguale a dim R-?
È forse dovuto al fatto che, in questo caso,
la matrice di transizione può essere singolare? (Luca Roffia)
 Il legame tra i sottospazi di raggiungibilità e di
controllabilità relativi allo stesso intervallo di tempo è
costituito dalla matrice di transizione relativa a tale intervallo. La
non singolarità di tale matrice assicura, nel caso continuo,
l'uguaglianza delle dimensioni di tali sottospazi. Nel caso
discreto, qualora la matrice di transizione risulti singolare, il
sottospazio di controllabilità avrà dimensione maggiore
di quello di raggiungibilità includendo anche lo spazio nullo
di tale matrice (si rivedano gli esempi fatti durante le lezioni).
Il legame tra i sottospazi di raggiungibilità e di
controllabilità relativi allo stesso intervallo di tempo è
costituito dalla matrice di transizione relativa a tale intervallo. La
non singolarità di tale matrice assicura, nel caso continuo,
l'uguaglianza delle dimensioni di tali sottospazi. Nel caso
discreto, qualora la matrice di transizione risulti singolare, il
sottospazio di controllabilità avrà dimensione maggiore
di quello di raggiungibilità includendo anche lo spazio nullo
di tale matrice (si rivedano gli esempi fatti durante le lezioni).
 #14
Nei sistemi dinamici lineari e non stazionari non ho ben capito il
legame tra le matrici dinamica e di distribuzione degli ingressi nel
passaggio dal modello continuo a quello discreto. (Luca Roffia) #14
Nei sistemi dinamici lineari e non stazionari non ho ben capito il
legame tra le matrici dinamica e di distribuzione degli ingressi nel
passaggio dal modello continuo a quello discreto. (Luca Roffia)
 Nella discretizzazione di un modello continuo la matrice
dinamica del modello discreto è semplicemente la matrice di
transizione di quello continuo negli intervalli considerati. Più
complessa la deduzione della matrice di distribuzione degli ingressi
del modello discreto che viene ricavata considerando l'espressione del
moto dei due modelli ed eguagliando gli stati iniziali e finali degli
intervalli di campionamento; supponendo la funzione di ingresso
costante in tali intervalli il contributo allo stato finale
dovuto al moto forzato nell'intervallo [kT,(k+1)T] può venire
espresso nella forma B(k)u(k) che definisce la matrice di distribuzione
degli ingressi, B(k), del modello discreto.
Nella discretizzazione di un modello continuo la matrice
dinamica del modello discreto è semplicemente la matrice di
transizione di quello continuo negli intervalli considerati. Più
complessa la deduzione della matrice di distribuzione degli ingressi
del modello discreto che viene ricavata considerando l'espressione del
moto dei due modelli ed eguagliando gli stati iniziali e finali degli
intervalli di campionamento; supponendo la funzione di ingresso
costante in tali intervalli il contributo allo stato finale
dovuto al moto forzato nell'intervallo [kT,(k+1)T] può venire
espresso nella forma B(k)u(k) che definisce la matrice di distribuzione
degli ingressi, B(k), del modello discreto.
 #15
Non ho ben capito quali sono le relazioni tra poli della funzione di
trasferimento e le caratteristiche del sistema in genere (poli ed
autovalori, poli e raggiungibilita' e/o osservabilita' ...).
(Alessandro Cevoli) #15
Non ho ben capito quali sono le relazioni tra poli della funzione di
trasferimento e le caratteristiche del sistema in genere (poli ed
autovalori, poli e raggiungibilita' e/o osservabilita' ...).
(Alessandro Cevoli)
 Si definiscono poli di un sistema dinamico lineare e stazionario
gli zeri dei denominatori degli
elementi della matrice (funzione) di trasferimento. Come sappiamo
(scomposizione canonica di Kalman), la funzione di trasferimento
descrive la sola parte raggiungibile ed osservabile del sistema;
i poli coincidono quindi con gli autovalori della matrice dinamica
associati a tale parte (= autovalori della sottomatrice A22
nella scomposizione canonica di Kalman).
Si definiscono poli di un sistema dinamico lineare e stazionario
gli zeri dei denominatori degli
elementi della matrice (funzione) di trasferimento. Come sappiamo
(scomposizione canonica di Kalman), la funzione di trasferimento
descrive la sola parte raggiungibile ed osservabile del sistema;
i poli coincidono quindi con gli autovalori della matrice dinamica
associati a tale parte (= autovalori della sottomatrice A22
nella scomposizione canonica di Kalman).
 #16
Considerando la banda passante della rete telefonica qual'è la
frequenza massima in bps che posso trasferirvi? (Alessandro Cevoli) #16
Considerando la banda passante della rete telefonica qual'è la
frequenza massima in bps che posso trasferirvi? (Alessandro Cevoli)
 La massima frequenza di cifra che può essere trasmessa con
probabilità di errore comunque piccola su un canale di banda B,
che opera con rapporto segnale/rumore S/N, (cioè la capacità
C del canale) è data dalla formula di Shannon
C=B*log2(1+S/N).
(Risposta a cura del prof. Leonardo Calandrino)
La massima frequenza di cifra che può essere trasmessa con
probabilità di errore comunque piccola su un canale di banda B,
che opera con rapporto segnale/rumore S/N, (cioè la capacità
C del canale) è data dalla formula di Shannon
C=B*log2(1+S/N).
(Risposta a cura del prof. Leonardo Calandrino)
 #17
Desidererei chiarimenti sull'argomento "poli dominanti di un sistema";
nella biblioteca ho trovato poche informazioni e per altro scritte male.
Grazie. (Lucio Vigness da Napoli) #17
Desidererei chiarimenti sull'argomento "poli dominanti di un sistema";
nella biblioteca ho trovato poche informazioni e per altro scritte male.
Grazie. (Lucio Vigness da Napoli)
 I poli dominanti vengono usualmente considerati quando si desidera
approssimare un modello di ordine elevato con un modello di ordine
ridotto, quando cioè si preferisce sostituire un modello esatto
ma complesso con un modello più semplice ma meno preciso.
La considerazione di base è la seguente: il moto e la risposta
di un sistema non sono influenzati nello stesso modo da tutti i modi
del sistema in quanto quelli che hanno una dinamica più
lenta "mascherano" (per così dire) quelli a dinamica più
veloce. Supponiamo allora di effettuare un cambiamento di base nello
spazio degli stati che porti la matrice dinamica del sistema alla
forma di Jordan; l'intero sistema può venire considerato ora
come formato da tanti sottosistemi collegati in parallelo, ognuno dei
quali con matrice dinamica data da un blocco di Jordan. Eliminiamo
ora tutti i sottosistemi associati agli autovalori cui corrispondono
modi ad evoluzione veloce (cioè quelli più lontani
dall'asse immaginario nel caso continuo, quelli a modulo minore
nel caso discreto) lasciando invece i rimanenti; il sistema che
si ottiene in questo modo ha solo una parte degli autovalori
(e dei poli) di quello iniziale e non ne descrive esattamente la
dinamica; in molti casi tuttavia il risultato (che dipende,
ovviamente, dalla entità dell'intervento e dalla
distribuzione degli autovalori del sistema) è del tutto
accettabile. Queste operazioni, descritte per un modello
nello spazio degli stati per maggior chiarezza, possono venire
effettuate direttamente sulla funzione di trasferimento del
sistema; queste tecniche sono state infatti introdotte proprio
con riferimento a modelli di questo tipo. Un modo diverso ma
sostanzialmente equivalente per valutare queste operazioni
consiste nel fare riferimento al contributo dato dai singoli
poli alla risposta frequenziale del sistema (diagrammi di
Bode, usati nell'ambito della teoria classica dei controlli
automatici). In questo contesto vengono eliminati dalla funzione
di trasferimento quei poli cui corrispondono frequenze di taglio
più elevate; è infatti evidente come la risposta
frequenziale dell'intero sistema sia condizionata in
primo luogo da quei poli cui corrispondono le frequenze di
taglio più basse. Le considerazioni precedenti sono
puramente qualitative e costituiscono solo una descrizione
introduttiva all'argomento citato; per una applicazione
non empirica vanno introdotte opportune funzioni costo che
forniscano una misura dello scostamento tra le prestazioni
del modello di ordine ridotto e quello iniziale. Tali
funzioni inoltre saranno, in genere, legate all'uso previsto
per il modello. Esistono, infine, molte altre tecniche di
approssimazione di un modello di ordine elevato con modelli
di ordine ridotto che risultano in genere più
efficaci di quella descritta in quanto non mantengono
una parte dei poli del modello iniziale in quello di ordine
ridotto.
I poli dominanti vengono usualmente considerati quando si desidera
approssimare un modello di ordine elevato con un modello di ordine
ridotto, quando cioè si preferisce sostituire un modello esatto
ma complesso con un modello più semplice ma meno preciso.
La considerazione di base è la seguente: il moto e la risposta
di un sistema non sono influenzati nello stesso modo da tutti i modi
del sistema in quanto quelli che hanno una dinamica più
lenta "mascherano" (per così dire) quelli a dinamica più
veloce. Supponiamo allora di effettuare un cambiamento di base nello
spazio degli stati che porti la matrice dinamica del sistema alla
forma di Jordan; l'intero sistema può venire considerato ora
come formato da tanti sottosistemi collegati in parallelo, ognuno dei
quali con matrice dinamica data da un blocco di Jordan. Eliminiamo
ora tutti i sottosistemi associati agli autovalori cui corrispondono
modi ad evoluzione veloce (cioè quelli più lontani
dall'asse immaginario nel caso continuo, quelli a modulo minore
nel caso discreto) lasciando invece i rimanenti; il sistema che
si ottiene in questo modo ha solo una parte degli autovalori
(e dei poli) di quello iniziale e non ne descrive esattamente la
dinamica; in molti casi tuttavia il risultato (che dipende,
ovviamente, dalla entità dell'intervento e dalla
distribuzione degli autovalori del sistema) è del tutto
accettabile. Queste operazioni, descritte per un modello
nello spazio degli stati per maggior chiarezza, possono venire
effettuate direttamente sulla funzione di trasferimento del
sistema; queste tecniche sono state infatti introdotte proprio
con riferimento a modelli di questo tipo. Un modo diverso ma
sostanzialmente equivalente per valutare queste operazioni
consiste nel fare riferimento al contributo dato dai singoli
poli alla risposta frequenziale del sistema (diagrammi di
Bode, usati nell'ambito della teoria classica dei controlli
automatici). In questo contesto vengono eliminati dalla funzione
di trasferimento quei poli cui corrispondono frequenze di taglio
più elevate; è infatti evidente come la risposta
frequenziale dell'intero sistema sia condizionata in
primo luogo da quei poli cui corrispondono le frequenze di
taglio più basse. Le considerazioni precedenti sono
puramente qualitative e costituiscono solo una descrizione
introduttiva all'argomento citato; per una applicazione
non empirica vanno introdotte opportune funzioni costo che
forniscano una misura dello scostamento tra le prestazioni
del modello di ordine ridotto e quello iniziale. Tali
funzioni inoltre saranno, in genere, legate all'uso previsto
per il modello. Esistono, infine, molte altre tecniche di
approssimazione di un modello di ordine elevato con modelli
di ordine ridotto che risultano in genere più
efficaci di quella descritta in quanto non mantengono
una parte dei poli del modello iniziale in quello di ordine
ridotto.
 #18
Dalla risposta da lei data alla domanda 13 si deduce che un sistema
stazionario con la matrice di transizione singolare abbia il sottospazio
di controllabilità di dimensione necessariamente maggiore di quella
del sottospazio di raggiungibilità, il che implicherebbe la non
completa raggiungibilità del sistema.
Questo, però, contraddice ciò che viene affermato nel
commento al primo test di pagina 7.3 del testo Teoria dei
Sistemi: Test commentati e risolti, in cui si afferma che la
singolarità della matrice di transizione non è condizione
preclusiva per la completa raggingibilità. (Mirko Tedaldi) #18
Dalla risposta da lei data alla domanda 13 si deduce che un sistema
stazionario con la matrice di transizione singolare abbia il sottospazio
di controllabilità di dimensione necessariamente maggiore di quella
del sottospazio di raggiungibilità, il che implicherebbe la non
completa raggiungibilità del sistema.
Questo, però, contraddice ciò che viene affermato nel
commento al primo test di pagina 7.3 del testo Teoria dei
Sistemi: Test commentati e risolti, in cui si afferma che la
singolarità della matrice di transizione non è condizione
preclusiva per la completa raggingibilità. (Mirko Tedaldi)
 La singolarità della matrice di transizione in un sistema lineare
stazionario e discreto certamente non preclude la completa
raggiungibilità; si pensi, ad esempio, al sistema
descritto dal modello x(k+1)=u(k), ove la matrice dinamica
(e quindi anche quella di transizione) è nulla e la matrice di
distribuzione degli ingressi è l'identità. La risposta
alla domanda 13 si riferisce, implicitamente, al caso in cui il
sistema non risulti completamente raggiungibile poiché,
in caso contrario, è immediato verificare come anche il
sottospazio di controllabilità coincida con l'intero spazio
degli stati. Se preferisce includere anche questo caso, può
sostituire il termine maggiore con non minore nella
risposta 13.
La singolarità della matrice di transizione in un sistema lineare
stazionario e discreto certamente non preclude la completa
raggiungibilità; si pensi, ad esempio, al sistema
descritto dal modello x(k+1)=u(k), ove la matrice dinamica
(e quindi anche quella di transizione) è nulla e la matrice di
distribuzione degli ingressi è l'identità. La risposta
alla domanda 13 si riferisce, implicitamente, al caso in cui il
sistema non risulti completamente raggiungibile poiché,
in caso contrario, è immediato verificare come anche il
sottospazio di controllabilità coincida con l'intero spazio
degli stati. Se preferisce includere anche questo caso, può
sostituire il termine maggiore con non minore nella
risposta 13.
 #19
Nel penultimo test a pagina 7.18 del testo Teoria dei
Sistemi: Test commentati e risolti, si afferma giustamente che la
memoria di un sistema discreto, lineare e stazionario, è minore
o uguale al grado del polinomio minimo di A. Questo comporta anche
che la memoria sia minore del grado del polinomio caratteristico di A,
però nella soluzione compare solo la risposta C, anziché B,C.
(Mirko Tedaldi) #19
Nel penultimo test a pagina 7.18 del testo Teoria dei
Sistemi: Test commentati e risolti, si afferma giustamente che la
memoria di un sistema discreto, lineare e stazionario, è minore
o uguale al grado del polinomio minimo di A. Questo comporta anche
che la memoria sia minore del grado del polinomio caratteristico di A,
però nella soluzione compare solo la risposta C, anziché B,C.
(Mirko Tedaldi)
 Le soluzioni corrette (B e C) sono da tempo presenti nella
Errata Corrige
del testo (presente nella sezione Testi
sul server). Approfitto dell'occasione per ricordare come sia utile
cancellare frequentemente la cache del browser o utilizzare
il tasto reload per evitare di vedersi proporre versioni
obsolete degli ipertesti presenti sul server. Una alternativa
può consistere nel ridurre drasticamente (configurando le
opzioni del browser) il tempo di latenza.
Le soluzioni corrette (B e C) sono da tempo presenti nella
Errata Corrige
del testo (presente nella sezione Testi
sul server). Approfitto dell'occasione per ricordare come sia utile
cancellare frequentemente la cache del browser o utilizzare
il tasto reload per evitare di vedersi proporre versioni
obsolete degli ipertesti presenti sul server. Una alternativa
può consistere nel ridurre drasticamente (configurando le
opzioni del browser) il tempo di latenza.
 #20
Nella matrice di risposta impulsiva devono sempre comparire tutti
i modi della parte raggiungibile e osservabile? Non potrebbe essere che
alcuni modi, data una particolare forma di A e B, scompaiano?
Se così fosse allora la risposta C all'ultimo test a pagina 7.61
del testo Teoria dei Sistemi: Test commentati e risolti, non sarebbe
vera. (Mirko Tedaldi) #20
Nella matrice di risposta impulsiva devono sempre comparire tutti
i modi della parte raggiungibile e osservabile? Non potrebbe essere che
alcuni modi, data una particolare forma di A e B, scompaiano?
Se così fosse allora la risposta C all'ultimo test a pagina 7.61
del testo Teoria dei Sistemi: Test commentati e risolti, non sarebbe
vera. (Mirko Tedaldi)
 Ogni modo della parte raggiungibile ed osservabile di un sistema dinamico
lineare è presente in almeno un elemento della matrice di risposta
impulsiva; la dimostrazione può seguire le stesse linee di quella
data per la matrice di transizione. Se tale proprietà non valesse,
la risposta impulsiva e la matrice di trasferimento non costituirebbero
descrizioni complete di tale parte del sistema.
Ogni modo della parte raggiungibile ed osservabile di un sistema dinamico
lineare è presente in almeno un elemento della matrice di risposta
impulsiva; la dimostrazione può seguire le stesse linee di quella
data per la matrice di transizione. Se tale proprietà non valesse,
la risposta impulsiva e la matrice di trasferimento non costituirebbero
descrizioni complete di tale parte del sistema.
 #21
Nell'ultimo test a pagina 7.62 del testo Teoria dei Sistemi: Test
commentati e risolti, perché l'integrale della risposta
impulsiva rappresenti la risposta forzata, non bisogna specificare che
il sistema sia puramente dinamico? (Mirko Tedaldi) #21
Nell'ultimo test a pagina 7.62 del testo Teoria dei Sistemi: Test
commentati e risolti, perché l'integrale della risposta
impulsiva rappresenti la risposta forzata, non bisogna specificare che
il sistema sia puramente dinamico? (Mirko Tedaldi)
 La domanda fa, in effetti, riferimento a sistemi puramente dinamici;
questo lo si deduce però solo dal commento ove viene riportata
l'espressione della risposta forzata. Nel testo deve quindi venire
specificato che il sistema è puramente dinamico; la variazione
è stata aggiunta alla
Errata Corrige del testo (nella sezione Testi).
La domanda fa, in effetti, riferimento a sistemi puramente dinamici;
questo lo si deduce però solo dal commento ove viene riportata
l'espressione della risposta forzata. Nel testo deve quindi venire
specificato che il sistema è puramente dinamico; la variazione
è stata aggiunta alla
Errata Corrige del testo (nella sezione Testi).
 #22
Non ho ben capito l'Errata Corrige
del libro Teoria dei Sistemi: Test commentati e risolti, relativa alla
pagina 7.28; probabilmente il conteggio delle righe deve essere effettuato
dal basso e non dall'alto, come è invece indicato.
Però se così fosse, sarebbe corretta l'affermazione
che un sistema, lineare e stazionario, discreto e stabile i.l.s.l.,
è anche asintoticamente stabile se è completamente
controllabile, il che non è vero dato che la completa
controllabilitè non implica necessariamente la completa
raggiungibilità. (Mirko Tedaldi) #22
Non ho ben capito l'Errata Corrige
del libro Teoria dei Sistemi: Test commentati e risolti, relativa alla
pagina 7.28; probabilmente il conteggio delle righe deve essere effettuato
dal basso e non dall'alto, come è invece indicato.
Però se così fosse, sarebbe corretta l'affermazione
che un sistema, lineare e stazionario, discreto e stabile i.l.s.l.,
è anche asintoticamente stabile se è completamente
controllabile, il che non è vero dato che la completa
controllabilitè non implica necessariamente la completa
raggiungibilità. (Mirko Tedaldi)
 Le righe vanno, in effetti, contate dal basso (la tredicesima dall'alto non
contiene risposte). Ciò posto, la risposta B è corretta
non perché la completa controllabilità implichi (nei
sistemi discreti) la completa raggiungibilità, ma perché,
in un sistema lineare stazionario discreto completamente controllabile e
stabile i.l.s.l., tutti i modi della parte non raggiungibile risultano
necessariamente asintoticamente stabili. La domanda in oggetto non è
tra le più facili.
Le righe vanno, in effetti, contate dal basso (la tredicesima dall'alto non
contiene risposte). Ciò posto, la risposta B è corretta
non perché la completa controllabilità implichi (nei
sistemi discreti) la completa raggiungibilità, ma perché,
in un sistema lineare stazionario discreto completamente controllabile e
stabile i.l.s.l., tutti i modi della parte non raggiungibile risultano
necessariamente asintoticamente stabili. La domanda in oggetto non è
tra le più facili.
 #23
Con riferimento all'esercizio 5 del testo Teoria dei Sistemi:
Esercizi e Applicazioni, cosa rappresenta il metacentro M e
quali forze vi agiscono?
In base a quale criterio è stato scelto il punto C rispetto
al quale vengono calcolati i momenti? (Andrea Pierini e Matteo
Piovaticci) #23
Con riferimento all'esercizio 5 del testo Teoria dei Sistemi:
Esercizi e Applicazioni, cosa rappresenta il metacentro M e
quali forze vi agiscono?
In base a quale criterio è stato scelto il punto C rispetto
al quale vengono calcolati i momenti? (Andrea Pierini e Matteo
Piovaticci)
 Il metacentro è il punto cui si può pensare applicata
la risultante delle spinte di galleggiamento agenti sulla sezione
considerata. Il punto C indica l'intersezione della sezione
considerata con l'asse di rotazione (longitudinale) dello scafo.
Il metacentro è il punto cui si può pensare applicata
la risultante delle spinte di galleggiamento agenti sulla sezione
considerata. Il punto C indica l'intersezione della sezione
considerata con l'asse di rotazione (longitudinale) dello scafo.
 #24
Con riferimento alla prima domanda di pag. 6.7 del testo Teoria dei
Sistemi: Test commentati e risolti, non capisco perché la
risposta esatta sia B; infatti sostituendo nella espressione dello stato
iniziale lì riportata prima l'espressione della risposta libera e
poi l'espressione di Q, si trova Q+Qx0 che
dovrebbe rappresentare la proiezione di x0 su
Im(QT) e non su Im(Q). (Andrea Pierini) #24
Con riferimento alla prima domanda di pag. 6.7 del testo Teoria dei
Sistemi: Test commentati e risolti, non capisco perché la
risposta esatta sia B; infatti sostituendo nella espressione dello stato
iniziale lì riportata prima l'espressione della risposta libera e
poi l'espressione di Q, si trova Q+Qx0 che
dovrebbe rappresentare la proiezione di x0 su
Im(QT) e non su Im(Q). (Andrea Pierini)
 Q, essendo simmetrica, coincide con la sua trasposta.
Q, essendo simmetrica, coincide con la sua trasposta.
 #25
Con riferimento al testo Teoria dei Sistemi: Test commentati e
risolti, e all'ultimo test di pag. 7.56, cosa si intende per
integratore? (Gabriele Tinti) #25
Con riferimento al testo Teoria dei Sistemi: Test commentati e
risolti, e all'ultimo test di pag. 7.56, cosa si intende per
integratore? (Gabriele Tinti)
 Un sistema la cui risposta forzata coincida con l'integrale della
funzione di ingresso. Sistemi di tale tipo, realizzati mediante
amplificatori operazionali, sono descritti negli esercizi 14 e 15
del testo Teoria dei Sistemi: Esercizi e Applicazioni.
Un sistema la cui risposta forzata coincida con l'integrale della
funzione di ingresso. Sistemi di tale tipo, realizzati mediante
amplificatori operazionali, sono descritti negli esercizi 14 e 15
del testo Teoria dei Sistemi: Esercizi e Applicazioni.
 #26
Con riferimento al testo Teoria dei Sistemi: Test commentati e
risolti, e al primo test di pag. 7.57, perché fra le
risposte esatte è da escludere la A? (Gabriele Tinti) #26
Con riferimento al testo Teoria dei Sistemi: Test commentati e
risolti, e al primo test di pag. 7.57, perché fra le
risposte esatte è da escludere la A? (Gabriele Tinti)
 Perché la condizione descritta da tale risposta non implica
affatto la nilpotenza della matrice dinamica. Consideri, ad esempio,
il sistema con matrice dinamica A=I e matrice di distribuzione degli
ingressi B=I; tale sistema risulta completamente controllabile ma
non soddisfa la condizione richiesta dalla domanda (ogni stato
risulta di equilibrio con ingresso nullo).
Perché la condizione descritta da tale risposta non implica
affatto la nilpotenza della matrice dinamica. Consideri, ad esempio,
il sistema con matrice dinamica A=I e matrice di distribuzione degli
ingressi B=I; tale sistema risulta completamente controllabile ma
non soddisfa la condizione richiesta dalla domanda (ogni stato
risulta di equilibrio con ingresso nullo).
 #27
Con riferimento all'esercizio 5 del testo Teoria dei Sistemi:
Esercizi e Applicazioni e alla D23), non riusciamo a capire
nell'equazione di bilancio delle coppie il termine relativo alle
spinte di galleggiamento: quanto valgono esattamente?
Inoltre in tale equzione J non dovrebbe rappresentare il momento
d'inerzia rispetto l'asse di rotazione anziché rispetto
all'asse baricentrico? (Andrea Pierini e Matteo Piovaticci) #27
Con riferimento all'esercizio 5 del testo Teoria dei Sistemi:
Esercizi e Applicazioni e alla D23), non riusciamo a capire
nell'equazione di bilancio delle coppie il termine relativo alle
spinte di galleggiamento: quanto valgono esattamente?
Inoltre in tale equzione J non dovrebbe rappresentare il momento
d'inerzia rispetto l'asse di rotazione anziché rispetto
all'asse baricentrico? (Andrea Pierini e Matteo Piovaticci)
 La risultante delle spinte di galleggiamento bilancia, ovviamente,
il peso del natante (mg) ma risulta applicata nel metacentro
anziché nel baricentro; un angolo di rollio diverso da zero
provoca quindi una coppia (si vedano le Osservazioni al termine
dell'esercizio). L'equazione di equilibrio delle coppie deriva,
con semplici passaggi, da tali considerazioni.
La risultante delle spinte di galleggiamento bilancia, ovviamente,
il peso del natante (mg) ma risulta applicata nel metacentro
anziché nel baricentro; un angolo di rollio diverso da zero
provoca quindi una coppia (si vedano le Osservazioni al termine
dell'esercizio). L'equazione di equilibrio delle coppie deriva,
con semplici passaggi, da tali considerazioni.
 #28
Vorremmo una ulteriore precisazione sull'esercizio 17 del testo
Teoria dei Sistemi: Esercizi e Applicazioni: dalla
Figura 17.3 emerge che il potenziale del morsetto di uscita
dell'amplificatore operazionele vale
V0=-R0i1+G(V--V+);
non dovrebbe essere
V0=-R0i1+G(V+-V-)?
(Andrea Pierini e Matteo Piovaticci) #28
Vorremmo una ulteriore precisazione sull'esercizio 17 del testo
Teoria dei Sistemi: Esercizi e Applicazioni: dalla
Figura 17.3 emerge che il potenziale del morsetto di uscita
dell'amplificatore operazionele vale
V0=-R0i1+G(V--V+);
non dovrebbe essere
V0=-R0i1+G(V+-V-)?
(Andrea Pierini e Matteo Piovaticci)
 Nella Figura 17.1 gli ingressi dell'operazionale sono scambiati
(si veda l'Errata Corrige del testo).
Nella Figura 17.1 gli ingressi dell'operazionale sono scambiati
(si veda l'Errata Corrige del testo).
 #29
Vorrei sapere come si può sfruttare la funzione di trasferimento
se è data nel dominio dei tempi; in altre parole y(t)=G(s)*u(t)
ove G(s) è una funzione razionale propria o strettamente
propria nell'operatore differenziale s.
Come si può calcolare, per esempio, y(t), con
u(t)=Vm*sen(omega*t)
senza passare per G(j*omega)? (Daniele Cremonini) #29
Vorrei sapere come si può sfruttare la funzione di trasferimento
se è data nel dominio dei tempi; in altre parole y(t)=G(s)*u(t)
ove G(s) è una funzione razionale propria o strettamente
propria nell'operatore differenziale s.
Come si può calcolare, per esempio, y(t), con
u(t)=Vm*sen(omega*t)
senza passare per G(j*omega)? (Daniele Cremonini)
 Va anzitutto rilevato come la funzione di trasferimento abbia la stessa
espressione sia se considerata nell'operatore differenziale (s
nel nostro caso), quindi nel dominio dei tempi, sia se espressa nella
variabile complessa s. Nel primo caso la funzione di trasferimento
descrive una equazione differenziale che lega l'uscita e le sue derivate
all'ingresso e alle relative derivate. Volendo quindi calcolare la risposta
ad un determinato ingresso nel dominio dei tempi sarà necessario
trovare la soluzione di tale equazione differenziale corrispondente alla
funzione di ingresso applicata ed alle condizioni iniziali del sistema.
Considerando la funzione di trasferimento come trasformata di Laplace
della risposta impulsiva del sistema è poi possibile,
antitrasformando la G(s), ottenere la W(t) e, nel dominio dei
tempi, la risposta a qualunque funzione di ingresso u(t) calcolando,
come abbiamo visto a lezione, un integrale di convoluzione; in questo
modo vengono considerate condizioni iniziali nulle (stato inziziale
zero) e viene calcolata la sola risposta forzata del sistema.
Un'ultima via consiste nel calcolare la L-trasformata, U(s), della
funzione di ingresso e nell'antitrasformare la trasformata di Laplace
della risposta (forzata) Y(s)=G(s)U(s). Le tre vie precedenti
utilizzano direttamente la funzione di trasferimento; è
naturalmente possibile anche ottenere una realizzazione nello
spazio degli stati della G(s) ed operare nel dominio dei tempi,
come abbiamo visto più volte, su tali rappresentazioni.
Va anzitutto rilevato come la funzione di trasferimento abbia la stessa
espressione sia se considerata nell'operatore differenziale (s
nel nostro caso), quindi nel dominio dei tempi, sia se espressa nella
variabile complessa s. Nel primo caso la funzione di trasferimento
descrive una equazione differenziale che lega l'uscita e le sue derivate
all'ingresso e alle relative derivate. Volendo quindi calcolare la risposta
ad un determinato ingresso nel dominio dei tempi sarà necessario
trovare la soluzione di tale equazione differenziale corrispondente alla
funzione di ingresso applicata ed alle condizioni iniziali del sistema.
Considerando la funzione di trasferimento come trasformata di Laplace
della risposta impulsiva del sistema è poi possibile,
antitrasformando la G(s), ottenere la W(t) e, nel dominio dei
tempi, la risposta a qualunque funzione di ingresso u(t) calcolando,
come abbiamo visto a lezione, un integrale di convoluzione; in questo
modo vengono considerate condizioni iniziali nulle (stato inziziale
zero) e viene calcolata la sola risposta forzata del sistema.
Un'ultima via consiste nel calcolare la L-trasformata, U(s), della
funzione di ingresso e nell'antitrasformare la trasformata di Laplace
della risposta (forzata) Y(s)=G(s)U(s). Le tre vie precedenti
utilizzano direttamente la funzione di trasferimento; è
naturalmente possibile anche ottenere una realizzazione nello
spazio degli stati della G(s) ed operare nel dominio dei tempi,
come abbiamo visto più volte, su tali rappresentazioni.
 #30
Perché una retroazione ingresso-uscita in un sistema lineare e
stazionario completamente raggiungibile ed osservabile non permette
di allocare ad arbitrio gli autovalori della matrice dinamica? #30
Perché una retroazione ingresso-uscita in un sistema lineare e
stazionario completamente raggiungibile ed osservabile non permette
di allocare ad arbitrio gli autovalori della matrice dinamica?
Le volevo chiedere se è esaustiva una risposta di questo tipo: Una
retroazione ingresso-uscita non permette di far retroagire tutte le
informazioni sullo stato e quindi posizionare ad arbitrio gli autovalori,
ma solo una parte di esse, poiché si fa retroagire una trasformazione
lineare dello stato secondo la matrice C, non lo stato stesso.
(Gabriele Tinti)
 La risposta che lei formula è sostanzialmente corretta.
Dalla scomposizione canonica di Kalman di un sistema generico è
immediato
verificare come una retroazione algebrica ingresso-uscita agisca
solo sulla parte raggiungibile ed osservabile del sistema. L'uscita in
un certo istante, d'altronde, non è detto fornisca una conoscenza
completa dello stato di tale parte.
La risposta che lei formula è sostanzialmente corretta.
Dalla scomposizione canonica di Kalman di un sistema generico è
immediato
verificare come una retroazione algebrica ingresso-uscita agisca
solo sulla parte raggiungibile ed osservabile del sistema. L'uscita in
un certo istante, d'altronde, non è detto fornisca una conoscenza
completa dello stato di tale parte.
 #31
Con riferimento alla R22) non ho capito perché
in un sistema lineare stazionario discreto
completamente controllabile e stabile i.l.s.l., i modi della
parte non raggiungibile risultano necessariamente
asintoticamente stabili. (Matteo Meucci) #31
Con riferimento alla R22) non ho capito perché
in un sistema lineare stazionario discreto
completamente controllabile e stabile i.l.s.l., i modi della
parte non raggiungibile risultano necessariamente
asintoticamente stabili. (Matteo Meucci)
 Se esistessero modi non asintoticamente stabili nella parte non
raggiungibile, quindi non influenzata dall'ingresso, esisterebbero
stati iniziali che darebbero luogo a moti instabili non riconducibili
all'origine mediante l'applicazione di una opportuna funzione di
ingresso. Facendo riferimento alla scomposizione canonica di Kalman,
basta osservare che i moti della parte non raggiungibile sono sempre
moti liberi; perché tali moti tendano all'origine occorre che
tale parte sia asintoticamente stabile.
Se esistessero modi non asintoticamente stabili nella parte non
raggiungibile, quindi non influenzata dall'ingresso, esisterebbero
stati iniziali che darebbero luogo a moti instabili non riconducibili
all'origine mediante l'applicazione di una opportuna funzione di
ingresso. Facendo riferimento alla scomposizione canonica di Kalman,
basta osservare che i moti della parte non raggiungibile sono sempre
moti liberi; perché tali moti tendano all'origine occorre che
tale parte sia asintoticamente stabile.
 #32
Con riferimento al secondo test di pagina 7.5 del testo Teoria dei
Sistemi: Test commentati e risolti,
non ho ben capito perché se un sistema lineare
stazionario discreto ha la matrice A nulla è
completamente ricostruibile. (Cristiano Gragnato) #32
Con riferimento al secondo test di pagina 7.5 del testo Teoria dei
Sistemi: Test commentati e risolti,
non ho ben capito perché se un sistema lineare
stazionario discreto ha la matrice A nulla è
completamente ricostruibile. (Cristiano Gragnato)
 Perché a partire da qualunque stato iniziale x0,
all'istante successivo ci si trova nello stato x1=Bu(0)
determinabile indipendentemente da x0.
Perché a partire da qualunque stato iniziale x0,
all'istante successivo ci si trova nello stato x1=Bu(0)
determinabile indipendentemente da x0.
 #33
Nella risposta al primo test di pagina 7.13 del testo Teoria dei
Sistemi: Test commentati e risolti, si dice
che uno stato di equilibrio con ingresso nullo
corrisponde ad un moto libero. Ciò non vale per
uno stato che non sia di equilibrio? (Cristiano Gragnato) #33
Nella risposta al primo test di pagina 7.13 del testo Teoria dei
Sistemi: Test commentati e risolti, si dice
che uno stato di equilibrio con ingresso nullo
corrisponde ad un moto libero. Ciò non vale per
uno stato che non sia di equilibrio? (Cristiano Gragnato)
 La traiettoria relativa ad un moto può coincidere con un singolo
stato, in un assegnato intervallo di tempo, solo se tale stato
risulta di equilibrio (con ingresso nullo o meno) nell'intervallo
considerato; diversamente la traiettoria sarà formata da una
sequenza di stati diversi e non da un solo stato.
La traiettoria relativa ad un moto può coincidere con un singolo
stato, in un assegnato intervallo di tempo, solo se tale stato
risulta di equilibrio (con ingresso nullo o meno) nell'intervallo
considerato; diversamente la traiettoria sarà formata da una
sequenza di stati diversi e non da un solo stato.
 #34
Con riferimento all'ultimo test di pagina 7.58 del testo Teoria dei
Sistemi: Test commentati e risolti,
non mi è chiaro come mai se la risposta forzata
risulta illimitata posso affermare che è
presente almeno un modo non asintoticamente
stabile. Io direi piuttosto che è presente
almeno un modo instabile (invalidando la risposta B). (Matteo Meucci) #34
Con riferimento all'ultimo test di pagina 7.58 del testo Teoria dei
Sistemi: Test commentati e risolti,
non mi è chiaro come mai se la risposta forzata
risulta illimitata posso affermare che è
presente almeno un modo non asintoticamente
stabile. Io direi piuttosto che è presente
almeno un modo instabile (invalidando la risposta B). (Matteo Meucci)
 È facile convincersi che la risposta corretta è quella
riportata facendo riferimento, ad esempio, ad un integratore, che dispone
di un solo modo semplicemente stabile (un solo polo nell'origine).
La risposta di tale sistema ad un ingresso costante (quindi limitato)
è una rampa (non limitata).
È facile convincersi che la risposta corretta è quella
riportata facendo riferimento, ad esempio, ad un integratore, che dispone
di un solo modo semplicemente stabile (un solo polo nell'origine).
La risposta di tale sistema ad un ingresso costante (quindi limitato)
è una rampa (non limitata).
 #35
Nel caso di sistemi lineari stazionari, nel calcolo del sottospazio di
raggiungibilità un'espressione del tipo BeAtx=0
essendo analitica, è nulla in [0,t1] se si
annulla in un punto dell'intervallo, quindi in tutto l'intervallo e
quindi anche in 0. Di qui lo sviluppo dell'espressione di R+
che risulta indipendente da t. Vorrei sapere se il fatto che l'annullarsi
in un punto implichi l'annullarsi in tutto l'intervallo, è dovuto
al fatto che il sistema è stazionario e quindi ogni valore di t
può essere preso come istante iniziale. (Vittorio Teglia) #35
Nel caso di sistemi lineari stazionari, nel calcolo del sottospazio di
raggiungibilità un'espressione del tipo BeAtx=0
essendo analitica, è nulla in [0,t1] se si
annulla in un punto dell'intervallo, quindi in tutto l'intervallo e
quindi anche in 0. Di qui lo sviluppo dell'espressione di R+
che risulta indipendente da t. Vorrei sapere se il fatto che l'annullarsi
in un punto implichi l'annullarsi in tutto l'intervallo, è dovuto
al fatto che il sistema è stazionario e quindi ogni valore di t
può essere preso come istante iniziale. (Vittorio Teglia)
 La analiticità della funzione di transizione costituisce, in
effetti, una delle conseguenze algebriche della stazionarietà
del sistema.
La analiticità della funzione di transizione costituisce, in
effetti, una delle conseguenze algebriche della stazionarietà
del sistema.
 #36
Non mi è chiaro perché prendendo come base dello spazio degli
stati la matrice T=[T1 T2] con
T1 base di R+ e T2
che completi una base dello spazio degli stati, la matrice di distribuzione
degli ingressi assuma la struttura T-1B =
[B1 0]T
in conseguenza del fatto che R+ è il minimo
invariante rispetto ad A che contiene Im(B) e non come logica
deduzione di B dal modello differenziale ottenuto dal cambio di base.
(Vittorio Teglia) #36
Non mi è chiaro perché prendendo come base dello spazio degli
stati la matrice T=[T1 T2] con
T1 base di R+ e T2
che completi una base dello spazio degli stati, la matrice di distribuzione
degli ingressi assuma la struttura T-1B =
[B1 0]T
in conseguenza del fatto che R+ è il minimo
invariante rispetto ad A che contiene Im(B) e non come logica
deduzione di B dal modello differenziale ottenuto dal cambio di base.
(Vittorio Teglia)
 Come ho sottolineato a lezione, la struttura di B rispetto alla base
considerata può venire dedotta indifferentemente in base a
considerazioni algebriche sulla nuova base (essendo T1
base di R+, le colonne di B in tale base avranno
componenti non nulle solo rispetto alle colonne di T1)
oppure geometriche, considerando cioè che Im(B) è
contenuto in R+.
Le considerazioni geometriche portano, in genere, ad una comprensione
più chiara delle proprietà.
Come ho sottolineato a lezione, la struttura di B rispetto alla base
considerata può venire dedotta indifferentemente in base a
considerazioni algebriche sulla nuova base (essendo T1
base di R+, le colonne di B in tale base avranno
componenti non nulle solo rispetto alle colonne di T1)
oppure geometriche, considerando cioè che Im(B) è
contenuto in R+.
Le considerazioni geometriche portano, in genere, ad una comprensione
più chiara delle proprietà.
 #37
Perché un sistema dinamico lineare e stazionario è
completamente raggiungibile se le righe di B corrispondenti a quelle
di A con un solo elemento diverso da 0 sono
linearmente indipendenti fra loro (nell'ambito di blocchi Jordan
relativi ad uno stesso autovalore)? (Vittorio Teglia) #37
Perché un sistema dinamico lineare e stazionario è
completamente raggiungibile se le righe di B corrispondenti a quelle
di A con un solo elemento diverso da 0 sono
linearmente indipendenti fra loro (nell'ambito di blocchi Jordan
relativi ad uno stesso autovalore)? (Vittorio Teglia)
 Si veda la risposta data alla D9).
Si veda la risposta data alla D9).
 #38
Vorrei sapere per quale motivo l'invertibilità della matrice di
transizione è una caratteristica intrinseca dei sistemi continui
mentre non lo è per quelli discreti? Da che cosa dipende questa
caratteristica? (Vittorio Teglia) #38
Vorrei sapere per quale motivo l'invertibilità della matrice di
transizione è una caratteristica intrinseca dei sistemi continui
mentre non lo è per quelli discreti? Da che cosa dipende questa
caratteristica? (Vittorio Teglia)
 Nei modelli continui la matrice di transizione è
data dall'esponenziale della matrice dinamica e tale funzione di
matrice è, come noto, sempre non singolare; nei modelli
discreti invece la matrice di transizione, essendo la potenza della
matrice dinamica, risulterà singolare quando lo è la
matrice dinamica. Tutto questo dal punto di vista matematico;
naturalmente se consideriamo il modello discreto di un sistema
continuo, la matrice dinamica coinciderà con l'esponenziale,
relativo all'intervallo di campionamento, della matrice dinamica del
modello continuo e sarà quindi sempre non singolare.
Nei modelli continui la matrice di transizione è
data dall'esponenziale della matrice dinamica e tale funzione di
matrice è, come noto, sempre non singolare; nei modelli
discreti invece la matrice di transizione, essendo la potenza della
matrice dinamica, risulterà singolare quando lo è la
matrice dinamica. Tutto questo dal punto di vista matematico;
naturalmente se consideriamo il modello discreto di un sistema
continuo, la matrice dinamica coinciderà con l'esponenziale,
relativo all'intervallo di campionamento, della matrice dinamica del
modello continuo e sarà quindi sempre non singolare.
 #39
Non mi è chiaro come, nel caso di sistemi lineari non stazionari
discreti, si determini il sottospazio R-(j,i,0) quando
la matrice di transizione è singolare; non potendo utilizzare
l'inversa di tale matrice posso forse utilizzare al suo posto una
funzione legata alla pseudoinversa? (Vittorio Teglia) #39
Non mi è chiaro come, nel caso di sistemi lineari non stazionari
discreti, si determini il sottospazio R-(j,i,0) quando
la matrice di transizione è singolare; non potendo utilizzare
l'inversa di tale matrice posso forse utilizzare al suo posto una
funzione legata alla pseudoinversa? (Vittorio Teglia)
 Quello che occorre calcolare è l'immagine inversa, secondo
la trasformazione lineare descritta dalla matrice di transizione,
del sottospazio R+(j,i,0). Si trasformerà quindi,
come abbiamo visto a lezione, R+(j,i,0) mediante la
pseudoinversa della matrice di transizione e si sommerà lo spazio
nullo della matrice di transizione stessa.
Quello che occorre calcolare è l'immagine inversa, secondo
la trasformazione lineare descritta dalla matrice di transizione,
del sottospazio R+(j,i,0). Si trasformerà quindi,
come abbiamo visto a lezione, R+(j,i,0) mediante la
pseudoinversa della matrice di transizione e si sommerà lo spazio
nullo della matrice di transizione stessa.
 #40
Retroazione stato-ingresso nei sistemi lineari e stazionari:
come vengono modificate le proprietà
di raggiungibilità e osservabilità?
In particolare perché R+(0) non è alterato
in dimensione e orientamento mentre il sottospazio di inosservabilità
può venire modificato? (Vittorio Teglia) #40
Retroazione stato-ingresso nei sistemi lineari e stazionari:
come vengono modificate le proprietà
di raggiungibilità e osservabilità?
In particolare perché R+(0) non è alterato
in dimensione e orientamento mentre il sottospazio di inosservabilità
può venire modificato? (Vittorio Teglia)
 Può verificare facilmente tali proprietà per via algebrica
facendo riferimento alla matrice dinamica del sistema chiuso in retroazione
(A + BK) ed alle espressioni dei sottospazi di raggiungibilità
e di inosservabilità, come abbiamo fatto a lezione. Considerando
la matrice dinamica in forma di Jordan ed il teorema relativo alle
condizioni di raggiungibilità ed osservabilità relativo a
tale rappresentazione si possono verificare, in maniera molto diretta,
le proprietà precedenti. Una ulteriore verifica della
invarianza del sottospazio di raggiungibilità rispetto ad
una retroazione stato-ingresso, si può ottenere facendo riferimento
alla scomposizione canonica di Kalman ed osservando che l'ingresso, non
potendo agire sulle parti non raggiungibili, non può modificare
le caratteristiche di raggiungibilità di tali parti.
Può verificare facilmente tali proprietà per via algebrica
facendo riferimento alla matrice dinamica del sistema chiuso in retroazione
(A + BK) ed alle espressioni dei sottospazi di raggiungibilità
e di inosservabilità, come abbiamo fatto a lezione. Considerando
la matrice dinamica in forma di Jordan ed il teorema relativo alle
condizioni di raggiungibilità ed osservabilità relativo a
tale rappresentazione si possono verificare, in maniera molto diretta,
le proprietà precedenti. Una ulteriore verifica della
invarianza del sottospazio di raggiungibilità rispetto ad
una retroazione stato-ingresso, si può ottenere facendo riferimento
alla scomposizione canonica di Kalman ed osservando che l'ingresso, non
potendo agire sulle parti non raggiungibili, non può modificare
le caratteristiche di raggiungibilità di tali parti.
 #41
Con riferimento al testo Teoria dei Sistemi: Esercizi e Applicazioni,
ed all'esercizio 20, vorrei sapere se nel modello la corrente coincide con
la potenza termica. Inoltre come è definita la potenza termica in
termini termodinamici? (Vittorio Teglia) #41
Con riferimento al testo Teoria dei Sistemi: Esercizi e Applicazioni,
ed all'esercizio 20, vorrei sapere se nel modello la corrente coincide con
la potenza termica. Inoltre come è definita la potenza termica in
termini termodinamici? (Vittorio Teglia)
 Il modello riportato in Figura 20.2 non è il modello
di una rete elettrica; non vi sono quindi correnti in gioco. Si può
tuttavia osservare che tale modello è analogo al modello
di una rete elettrica nella quale le correnti corrispondano alle potenze
che attraversano i vari rami nel modello del sistema termico.
La potenza può venire indifferentemente definita come lavoro,
energia o quantità di calore nell'unità di tempo e quindi
venire espressa utilizzando unità diverse, tutte comunque
riconducibili a watt cioè a Joule/s (m2*
kg*s-3).
Il modello riportato in Figura 20.2 non è il modello
di una rete elettrica; non vi sono quindi correnti in gioco. Si può
tuttavia osservare che tale modello è analogo al modello
di una rete elettrica nella quale le correnti corrispondano alle potenze
che attraversano i vari rami nel modello del sistema termico.
La potenza può venire indifferentemente definita come lavoro,
energia o quantità di calore nell'unità di tempo e quindi
venire espressa utilizzando unità diverse, tutte comunque
riconducibili a watt cioè a Joule/s (m2*
kg*s-3).
 #42
Date le matrici A,B,C,D di un sistema dinamico, in un esercizio
vengono richiesti gli autovalori della forma minima.
Ho calcolato una base del sottospazio di inosservabilità
ed ho effettuato la separazione del sistema in parte osservabile
e in parte inosservabile.
Poi ho calcolato gli autovalori della parte osservabile e con
questo dovrei avere terminato.
C'è un metodo più rapido?
In particolare è sempre indispensabile
effettuare il cambiamento di base con T-1AT o tale passaggio
può essere omesso sfruttando le proprietà degli endomorfismi?
Il dubbio mi viene perché ricordo che a lezione ha detto che se la
matrice T è ortonormale allora qualcosa (che non ricordo) si
riduce ad una permutazione delle righe/colonne di A. (Daniele Cremonini) #42
Date le matrici A,B,C,D di un sistema dinamico, in un esercizio
vengono richiesti gli autovalori della forma minima.
Ho calcolato una base del sottospazio di inosservabilità
ed ho effettuato la separazione del sistema in parte osservabile
e in parte inosservabile.
Poi ho calcolato gli autovalori della parte osservabile e con
questo dovrei avere terminato.
C'è un metodo più rapido?
In particolare è sempre indispensabile
effettuare il cambiamento di base con T-1AT o tale passaggio
può essere omesso sfruttando le proprietà degli endomorfismi?
Il dubbio mi viene perché ricordo che a lezione ha detto che se la
matrice T è ortonormale allora qualcosa (che non ricordo) si
riduce ad una permutazione delle righe/colonne di A. (Daniele Cremonini)
 Il procedimento da lei seguito è corretto ed applicabile in
generale. Quando il sottospazio di inosservabilità,
E-(0,0), ammette una base costituita da alcune colonne
(non necessariamente adiacenti) della matrice identità, la
scomposizione del sistema in parte osservabile (forma minima) e
parte non osservabile può venire effettuata selezionando
opportunamente gli elementi delle matrici A, B e C; in tale
caso infatti le matrici T-1 e T, se costruite con
colonne dell'identità (pur essendo questa la scelta più
consigliabile, non è l'unica possibile),
effettuano solo permutazioni di righe e di colonne.
Il procedimento è stato esemplificato, anche in relazione
alla scomposizione del sistema in parte raggiungibile e non raggiungibile
ed alla scomposizione canonica di Kalman, in vari esercizi svolti durante
il corso.
Il procedimento da lei seguito è corretto ed applicabile in
generale. Quando il sottospazio di inosservabilità,
E-(0,0), ammette una base costituita da alcune colonne
(non necessariamente adiacenti) della matrice identità, la
scomposizione del sistema in parte osservabile (forma minima) e
parte non osservabile può venire effettuata selezionando
opportunamente gli elementi delle matrici A, B e C; in tale
caso infatti le matrici T-1 e T, se costruite con
colonne dell'identità (pur essendo questa la scelta più
consigliabile, non è l'unica possibile),
effettuano solo permutazioni di righe e di colonne.
Il procedimento è stato esemplificato, anche in relazione
alla scomposizione del sistema in parte raggiungibile e non raggiungibile
ed alla scomposizione canonica di Kalman, in vari esercizi svolti durante
il corso.
 #43
Come si fa ad ottenere la struttura della matrice dinamica A+BH di
un sistema dinamico lineare stazionario retroazionato stato-ingresso secondo
la scomposizione di Kalman (dagli appunti mi risulta che BH agisca
solo su A11 con B1H1 e su
A22 con B2H2; dove sono i
termini B1H2, B1H3,
B1H4, B2H1,
B2H3 e B2H4?).
(Cristiano Carretti) #43
Come si fa ad ottenere la struttura della matrice dinamica A+BH di
un sistema dinamico lineare stazionario retroazionato stato-ingresso secondo
la scomposizione di Kalman (dagli appunti mi risulta che BH agisca
solo su A11 con B1H1 e su
A22 con B2H2; dove sono i
termini B1H2, B1H3,
B1H4, B2H1,
B2H3 e B2H4?).
(Cristiano Carretti)
 Assumendo, come lei opportunamente fa, la matrice H partizionata
in maniera congruente con la matrice dinamica, è immediato verificare
come gli 8 termini non nulli che nascono nel prodotto di B e H
vadano a sommarsi agli elementi delle prime due righe (a blocchi) di A;
l'azione di BH non è quindi limitata alle sole sottomatrici
A11 e A22.
L'esame della struttura della matrice dinamica del sistema retroazionato
consente di verificare l'invarianza, rispetto a tale operazione, del
sottospazio di raggiungibilità ed evidenzia anche
come tale matrice non corrisponda più ad una scomposizione
di Kalman del sistema; questo risultato è d'altronde ben noto
poiché una retroazione stato-ingresso può modificare
dimensione ed orientamento del sottospazio di inosservabilità.
Per ottenere la scomposizione di Kalman del sistema retroazionato
sarà quindi necessario applicare la relativa procedura alla
terna di matrici ((A+BH),B,C).
Assumendo, come lei opportunamente fa, la matrice H partizionata
in maniera congruente con la matrice dinamica, è immediato verificare
come gli 8 termini non nulli che nascono nel prodotto di B e H
vadano a sommarsi agli elementi delle prime due righe (a blocchi) di A;
l'azione di BH non è quindi limitata alle sole sottomatrici
A11 e A22.
L'esame della struttura della matrice dinamica del sistema retroazionato
consente di verificare l'invarianza, rispetto a tale operazione, del
sottospazio di raggiungibilità ed evidenzia anche
come tale matrice non corrisponda più ad una scomposizione
di Kalman del sistema; questo risultato è d'altronde ben noto
poiché una retroazione stato-ingresso può modificare
dimensione ed orientamento del sottospazio di inosservabilità.
Per ottenere la scomposizione di Kalman del sistema retroazionato
sarà quindi necessario applicare la relativa procedura alla
terna di matrici ((A+BH),B,C).
 #44
Nell'esercizio 2 della sessione autunnale del 1995 presente nella sezione
Temi d'esame, si chiede di determinare il valore di k della retroazione
uscita-ingresso che corrisponda al limite della stabilità.
Ho costruito la matrice A+BKC ed ho ottenuto il polinomio caratteristico
p(l)=l2+7l-k.
Per valutare il limite della stabilità devo trovare il valore di k
che mi porta ad una permanenza di segno nell'equazione caratteristica
(cioè k<0)? (Nicola Garofalo) #44
Nell'esercizio 2 della sessione autunnale del 1995 presente nella sezione
Temi d'esame, si chiede di determinare il valore di k della retroazione
uscita-ingresso che corrisponda al limite della stabilità.
Ho costruito la matrice A+BKC ed ho ottenuto il polinomio caratteristico
p(l)=l2+7l-k.
Per valutare il limite della stabilità devo trovare il valore di k
che mi porta ad una permanenza di segno nell'equazione caratteristica
(cioè k<0)? (Nicola Garofalo)
 Deve trovare il valore limite che esclude la presenza di modi instabili nel
sistema; per il polinomio caratteristico da lei calcolato, essendo il sistema
in esame continuo,
tale valore è k=0; la risposta k<0 non può venire
considerata corretta. La informo inoltre che è superfluo
inviare ripetutamente le domande al server; la ricevuta di ritorno viene
infatti inviata solo dopo la scrittura dei messaggi ricevuti sul disco
rigido ed assicura quindi la corretta ricezione di quanto inviato (questo
vale, ovviamente, anche per la messa in lista).
Deve trovare il valore limite che esclude la presenza di modi instabili nel
sistema; per il polinomio caratteristico da lei calcolato, essendo il sistema
in esame continuo,
tale valore è k=0; la risposta k<0 non può venire
considerata corretta. La informo inoltre che è superfluo
inviare ripetutamente le domande al server; la ricevuta di ritorno viene
infatti inviata solo dopo la scrittura dei messaggi ricevuti sul disco
rigido ed assicura quindi la corretta ricezione di quanto inviato (questo
vale, ovviamente, anche per la messa in lista).
 #45
In riferimento all'esercizio 1 della sessione invernale 1997 presente nella
sezione Temi d'esame, ho ottenuto il seguente modello nello spazio
degli stati per il circuito proposto: #45
In riferimento all'esercizio 1 della sessione invernale 1997 presente nella
sezione Temi d'esame, ho ottenuto il seguente modello nello spazio
degli stati per il circuito proposto:
u/R1+C1*d(x1)/dt+x1/R2+
x2/R4=0
x1/R3+C2*d(x2)/dt=0
L'uscita, dipende solo da x2 oppure anche x1 influisce
in qualche modo? (Nicola Garofalo)
 L'esame del circuito evidenzia come, assumendo gli amplificatori operazionali
come ideali, l'uscita del sistema coincida con
x2, quindi l'equazione d'uscita è y=x2.
Ovviamente l'evoluzione nel tempo di x2 è influenzata
dalla evoluzione di x1 e quindi dall'andamento della funzione
di ingresso.
L'esame del circuito evidenzia come, assumendo gli amplificatori operazionali
come ideali, l'uscita del sistema coincida con
x2, quindi l'equazione d'uscita è y=x2.
Ovviamente l'evoluzione nel tempo di x2 è influenzata
dalla evoluzione di x1 e quindi dall'andamento della funzione
di ingresso.
 #46
Nell'esercizio 5 dell'appello estivo del 1996, la matrice B', dalla
quale poi si ricaverà B, è fatta nel seguente modo? #46
Nell'esercizio 5 dell'appello estivo del 1996, la matrice B', dalla
quale poi si ricaverà B, è fatta nel seguente modo?
B' = [ c 0 ]T
(Nicola Garofalo)
 Se si utilizza l'algoritmo di realizzazione per modelli puramente dinamici
che abbiamo visto a lezione, la matrice B' è formata, nel caso di
sistemi con un solo ingresso, da una sola colonna che contiene i coefficienti
del polinomio P(z) ordinati a partire dalla potenza di grado 0. Nel caso in
esame è quindi corretta quella da lei indicata; può
trovare la struttura di B' a pag. 29.3 del testo Teoria dei Sistemi:
Esercizi e applicazioni.
Se si utilizza l'algoritmo di realizzazione per modelli puramente dinamici
che abbiamo visto a lezione, la matrice B' è formata, nel caso di
sistemi con un solo ingresso, da una sola colonna che contiene i coefficienti
del polinomio P(z) ordinati a partire dalla potenza di grado 0. Nel caso in
esame è quindi corretta quella da lei indicata; può
trovare la struttura di B' a pag. 29.3 del testo Teoria dei Sistemi:
Esercizi e applicazioni.
 #47
Nel primo test di pagina 7.18 del testo Teoria dei Sistemi: Test
commentati e risolti, è indicata come corretta la sola
risposta B; perché non vanno ritenute esatte anche la A e la C?
(Terenzio Berni) #47
Nel primo test di pagina 7.18 del testo Teoria dei Sistemi: Test
commentati e risolti, è indicata come corretta la sola
risposta B; perché non vanno ritenute esatte anche la A e la C?
(Terenzio Berni)
 Perché ogni moto libero di un sistema lineare, stazionario e
discreto raggiunga lo stato zero in un numero finito di passi è
necessario che la matrice dinamica del sistema sia nilpotente; tale
condizione non è assicurata né dalla risposta A né
dalla C.
Perché ogni moto libero di un sistema lineare, stazionario e
discreto raggiunga lo stato zero in un numero finito di passi è
necessario che la matrice dinamica del sistema sia nilpotente; tale
condizione non è assicurata né dalla risposta A né
dalla C.
 #48
Con riferimento alla risposta al primo test di pagina 7.35 del testo
Teoria dei Sistemi: Test commentati e risolti, mi sono
chiesto se la molteplicità degli autovalori del polinomio minimo della
connessione in
cascata può essere diversa dalla molteplicità degli autovalori
nei polinomi caratteristici dei singoli sistemi disgiunti ed in
particolare minore. (Terenzio Berni) #48
Con riferimento alla risposta al primo test di pagina 7.35 del testo
Teoria dei Sistemi: Test commentati e risolti, mi sono
chiesto se la molteplicità degli autovalori del polinomio minimo della
connessione in
cascata può essere diversa dalla molteplicità degli autovalori
nei polinomi caratteristici dei singoli sistemi disgiunti ed in
particolare minore. (Terenzio Berni)
 Per rispondere al suo dubbio basta pensare alla struttura della matrice
dinamica della connessione in cascata che risulta triangolare a blocchi
con blocchi sulla diagonale principale costituiti dalle matrici dinamiche
dei due sistemi.
Poiché tale struttura si mantiene anche nell'esponenziale di questa
matrice, ne segue che la molteplicità degli autovalori
del relativo polinomio minimo può anche eguagliare la somma
delle loro molteplicità come zeri dei singoli polinomi caratteristici
(può trovare un esempio di tale situazione nell'Esercizio 14 del testo
Teoria dei Sistemi: Esercizi e Applicazioni) e non può
scendere al di sotto della massima tra le molteplicità relative
ai due polinomi minimi.
Per rispondere al suo dubbio basta pensare alla struttura della matrice
dinamica della connessione in cascata che risulta triangolare a blocchi
con blocchi sulla diagonale principale costituiti dalle matrici dinamiche
dei due sistemi.
Poiché tale struttura si mantiene anche nell'esponenziale di questa
matrice, ne segue che la molteplicità degli autovalori
del relativo polinomio minimo può anche eguagliare la somma
delle loro molteplicità come zeri dei singoli polinomi caratteristici
(può trovare un esempio di tale situazione nell'Esercizio 14 del testo
Teoria dei Sistemi: Esercizi e Applicazioni) e non può
scendere al di sotto della massima tra le molteplicità relative
ai due polinomi minimi.
 #49
Ho scritto negli appunti che due stati di sistemi lineari sono
indistinguibili quando danno luogo a risposte libere uguali. Secondo me
non è corretto. Perché, se le risposte libere sono uguali,
non posso dire che i due stati sono equivalenti ma devo limitarmi a dire
che sono indistinguibili? (Gianni Rondinini) #49
Ho scritto negli appunti che due stati di sistemi lineari sono
indistinguibili quando danno luogo a risposte libere uguali. Secondo me
non è corretto. Perché, se le risposte libere sono uguali,
non posso dire che i due stati sono equivalenti ma devo limitarmi a dire
che sono indistinguibili? (Gianni Rondinini)
 Gli stati che, in un sistema lineare, generano risposte libere uguali
sono ovviamente equivalenti essendo, in tali sistemi, additivo il
moto forzato. Stati equivalenti sono, naturalmente, anche indistinguibili
su ogni intervallo.
Gli stati che, in un sistema lineare, generano risposte libere uguali
sono ovviamente equivalenti essendo, in tali sistemi, additivo il
moto forzato. Stati equivalenti sono, naturalmente, anche indistinguibili
su ogni intervallo.
 #50
Ho scritto negli appunti che l'insieme E+(0,0) di un generico sistema
potrebbe avere più di un elemento anche se l'insieme E-(0,0)
ne ha uno solo. Non riesco a capire bene il motivo: è forse perché
il sistema potrebbe essere tempovariante? (Gianni Rondinini) #50
Ho scritto negli appunti che l'insieme E+(0,0) di un generico sistema
potrebbe avere più di un elemento anche se l'insieme E-(0,0)
ne ha uno solo. Non riesco a capire bene il motivo: è forse perché
il sistema potrebbe essere tempovariante? (Gianni Rondinini)
 La proprietà cui lei credo faccia riferimento è formulata in
termini opposti; può infatti accadere che E+(0,0) contenga
un solo elemento ed E-(0,0) ne contenga più di uno, ma non
l'inverso, a causa della unicità del moto generato da uno stato
iniziale e da una funzione di ingresso.
Ciò avviene quando la matrice di transizione del sistema è
singolare e questo è possibile nei sistemi discreti (ma
non nei modelli discreti dei sistemi continui). Se riguarda i suoi
appunti troverà un esempio limite che vi ho fatto a lezione,
relativo ad un sistema stazionario ed a tempo discreto nel quale
E+(0,0) contiene un solo elemento mentre E-(0,0)
coincide con l'intero spazio degli stati.
La proprietà cui lei credo faccia riferimento è formulata in
termini opposti; può infatti accadere che E+(0,0) contenga
un solo elemento ed E-(0,0) ne contenga più di uno, ma non
l'inverso, a causa della unicità del moto generato da uno stato
iniziale e da una funzione di ingresso.
Ciò avviene quando la matrice di transizione del sistema è
singolare e questo è possibile nei sistemi discreti (ma
non nei modelli discreti dei sistemi continui). Se riguarda i suoi
appunti troverà un esempio limite che vi ho fatto a lezione,
relativo ad un sistema stazionario ed a tempo discreto nel quale
E+(0,0) contiene un solo elemento mentre E-(0,0)
coincide con l'intero spazio degli stati.
 #51
In riferimento alla domanda 4 dell'Esercizio 4 della Sessione Autunnale '96
vorrei sapere se la risposta x(2)=[a b 0 0 ]T è corretta.
Ho dedotto tale risposta dall'osservazione di R+(0).
Ho poi calcolato la sequenza di ingresso dalla relazione
x(2)=[B AB][u(1) u(0)]T
Vorrei sapere se il ragionamento seguito è corretto ed avere
eventualmente l'indicazione di un modo di procedere generale.
(Michele Berionni) #51
In riferimento alla domanda 4 dell'Esercizio 4 della Sessione Autunnale '96
vorrei sapere se la risposta x(2)=[a b 0 0 ]T è corretta.
Ho dedotto tale risposta dall'osservazione di R+(0).
Ho poi calcolato la sequenza di ingresso dalla relazione
x(2)=[B AB][u(1) u(0)]T
Vorrei sapere se il ragionamento seguito è corretto ed avere
eventualmente l'indicazione di un modo di procedere generale.
(Michele Berionni)
 Lo stato raggiungibile dallo stato zero più vicino ad uno stato
assegnato è, in generale, la proiezione ortogonale di tale stato
su R+(0); il procedimento da lei seguito è quindi
corretto. Anche la sequenza di ingresso necessaria può venire
ricavata da una relazione del tipo da lei indicato; tale calcolo
richiederà, in generale, la pseudoinversione di una
matrice.
Lo stato raggiungibile dallo stato zero più vicino ad uno stato
assegnato è, in generale, la proiezione ortogonale di tale stato
su R+(0); il procedimento da lei seguito è quindi
corretto. Anche la sequenza di ingresso necessaria può venire
ricavata da una relazione del tipo da lei indicato; tale calcolo
richiederà, in generale, la pseudoinversione di una
matrice.
 #52
In riferimento alla domanda 2 dell'Esercizio 3 della Sessione Estiva '94,
ottengo affiancando Q trasposta alla matrice identità il seguente
risultato: #52
In riferimento alla domanda 2 dell'Esercizio 3 della Sessione Estiva '94,
ottengo affiancando Q trasposta alla matrice identità il seguente
risultato:
0 e | 1 0 0 GS 0 1 | 1 0 0
0 e | 0 1 0 --> 0 1 | 0 1 0
1 0 | 0 0 1 1 0 | 0 0 1
da cui sembrerebbe potersi dedurre che la base cercata è data dalle
prime due colonne della matrice identità.
Dall'osservazione delle matrici A,B,C sembra invece potersi dedurre che
il sistema è completamente osservabile:
| -d 0 0 |
A = | 0 -d 0 |
| e e 0 |
C = | 0 0 1 |
Vorrei sapere dove sbaglio.
(Michele Berionni)
 Nella valutazione della osservabilità osservando le matrici A e C.
Dato che non indica che criterio abbia seguito (A non è in
forma di Jordan) non è possibile risalire alla causa dell'errore.
Le segnalo anche che i vettori alla destra della freccia non
sono il risultato dell'applicazione della ortonormalizzazione di
Gram-Schmidt al gruppo di vettori a sinistra, per più di un
motivo (non sono infatti né ortonormali né indipendenti).
Nella valutazione della osservabilità osservando le matrici A e C.
Dato che non indica che criterio abbia seguito (A non è in
forma di Jordan) non è possibile risalire alla causa dell'errore.
Le segnalo anche che i vettori alla destra della freccia non
sono il risultato dell'applicazione della ortonormalizzazione di
Gram-Schmidt al gruppo di vettori a sinistra, per più di un
motivo (non sono infatti né ortonormali né indipendenti).
 #53
In riferimento alla domanda 1 dell'Esercizio 2 della Sessione Estiva '94
vorrei sapere se è corretto, dall'osservazione delle matrici B,C,
ridurre il calcolo di (sI-A)-1 a quello del complemento algebrico
dell'elemento (3,3) (diviso, naturalmente, per det(sI-A)).
Ottengo come risultato finale G(s)=s.
(Michele Berionni) #53
In riferimento alla domanda 1 dell'Esercizio 2 della Sessione Estiva '94
vorrei sapere se è corretto, dall'osservazione delle matrici B,C,
ridurre il calcolo di (sI-A)-1 a quello del complemento algebrico
dell'elemento (3,3) (diviso, naturalmente, per det(sI-A)).
Ottengo come risultato finale G(s)=s.
(Michele Berionni)
 Il procedimento seguito è corretto; può essere utile anche
ricordare, nel calcolo della matrice di trasferimento, che tale matrice
è determinata dalla sola parte raggiungibile ed osservabile del
sistema. La funzione di trasferimento che ottiene è però
sbagliata (corrisponderebbe, tra l'altro, ad un sistema anticipativo);
quella corretta è G(s)=1/s.
Il procedimento seguito è corretto; può essere utile anche
ricordare, nel calcolo della matrice di trasferimento, che tale matrice
è determinata dalla sola parte raggiungibile ed osservabile del
sistema. La funzione di trasferimento che ottiene è però
sbagliata (corrisponderebbe, tra l'altro, ad un sistema anticipativo);
quella corretta è G(s)=1/s.
 #54
In riferimento all'Esercizio 2 della Sessione Autunnale '95
ottengo, risolvendo la domanda 5, p(i)=i2+ic+ie+ec-k
(e,c = cifre del
numero di matricola) risultato che differisce (almeno per il termine ec)
da quello presentato in un'altra domanda da un altro studente.
Vorrei sapere, se possibile, se il mio risultato è corretto e se, in
questo caso, è giusto rispondere k=ec.
(Michele Berionni) #54
In riferimento all'Esercizio 2 della Sessione Autunnale '95
ottengo, risolvendo la domanda 5, p(i)=i2+ic+ie+ec-k
(e,c = cifre del
numero di matricola) risultato che differisce (almeno per il termine ec)
da quello presentato in un'altra domanda da un altro studente.
Vorrei sapere, se possibile, se il mio risultato è corretto e se, in
questo caso, è giusto rispondere k=ec.
(Michele Berionni)
 Il risultato da lei ottenuto non è corretto non essendo corretta
l'espressione del polinomio caratteristico del sistema in retroazione.
Il valore di k che avrebbe dovuto ottenere è k=c2.
Il risultato da lei ottenuto non è corretto non essendo corretta
l'espressione del polinomio caratteristico del sistema in retroazione.
Il valore di k che avrebbe dovuto ottenere è k=c2.
 #55
Nel secondo test di pagina 7.13 del libro Teoria dei Sistemi:
Test commentati e risolti vengono indicate come risposte corrette
A e C. Sulla A non ho dubbi, mentre la C, a mio avviso, è
errata: il fatto che un sistema possa ammettere forma minima di ordine
inferiore è compatibile (secondo me) con l'assenza di una parte non
raggiungibile e non osservabile.
Si consideri per esempio il sistema descritto dalle seguenti matrici A,B,C: #55
Nel secondo test di pagina 7.13 del libro Teoria dei Sistemi:
Test commentati e risolti vengono indicate come risposte corrette
A e C. Sulla A non ho dubbi, mentre la C, a mio avviso, è
errata: il fatto che un sistema possa ammettere forma minima di ordine
inferiore è compatibile (secondo me) con l'assenza di una parte non
raggiungibile e non osservabile.
Si consideri per esempio il sistema descritto dalle seguenti matrici A,B,C:
x x 0 0 x
x x 0 0 0
x x x x 0
x x x x 0
x 0 0 0
0 x 0 0
dove le x rappresentano valori arbitrari. Questo sistema ammette forma minima
di ordine 2 ed ha due soli blocchi nella scomposizione di Kalman, i blocchi
1 e 2, e quindi non ammette una parte non raggiungibile e non osservabile.
(Andrea Tassinari)
 Se rilegge con maggiore attenzione il testo della domanda, si accorgerà
che si fa riferimento ad una condizione sufficiente (... quando:)
e non necessaria e sufficiente come succederebbe se il testo fosse
del tipo ... solo quando:
Se rilegge con maggiore attenzione il testo della domanda, si accorgerà
che si fa riferimento ad una condizione sufficiente (... quando:)
e non necessaria e sufficiente come succederebbe se il testo fosse
del tipo ... solo quando:
 #56
In un sistema composto da due sottosistemi lineari completamente raggiungibili
connessi in parallelo fra di loro, ho degli elementi sui singoli
sottosistemi che mi possano garantire la completa raggiungibilità
dell'intero sistema?
(Federico Dall'Olio) #56
In un sistema composto da due sottosistemi lineari completamente raggiungibili
connessi in parallelo fra di loro, ho degli elementi sui singoli
sottosistemi che mi possano garantire la completa raggiungibilità
dell'intero sistema?
(Federico Dall'Olio)
 Se si escludono strutture particolari (es. Jordan) delle matrici dinamiche
di tali sottosistemi, la condizione resta quella del rango massimo della
matrice di controllabilità del sistema complessivo.
Se si escludono strutture particolari (es. Jordan) delle matrici dinamiche
di tali sottosistemi, la condizione resta quella del rango massimo della
matrice di controllabilità del sistema complessivo.
 #57
Un sistema discreto in cui la matrice di transizione è singolare,
è sempre riconducibile ad un sistema continuo?
(Federico Dall'Olio) #57
Un sistema discreto in cui la matrice di transizione è singolare,
è sempre riconducibile ad un sistema continuo?
(Federico Dall'Olio)
 Come abbiamo sottolineato più volte a lezione, la matrice dinamica
del modello discreto di un sistema continuo è sempre
non singolare e l'operazione da lei proposta non ammette soluzione.
Veda, a tale riguardo, anche l'esercizio 28 del testo Teoria dei Sistemi:
Esercizi e applicazioni.
Come abbiamo sottolineato più volte a lezione, la matrice dinamica
del modello discreto di un sistema continuo è sempre
non singolare e l'operazione da lei proposta non ammette soluzione.
Veda, a tale riguardo, anche l'esercizio 28 del testo Teoria dei Sistemi:
Esercizi e applicazioni.
 #58
In riferimento alla seconda domanda del primo esercizio della prova d'esame
del Luglio 1996, quando si chiede: "Si progetti la matrice K dei guadagni di
un osservatore dello stato con autovalori ....", a che osservatore ci si
riferisce? (Giorgio Grillini) #58
In riferimento alla seconda domanda del primo esercizio della prova d'esame
del Luglio 1996, quando si chiede: "Si progetti la matrice K dei guadagni di
un osservatore dello stato con autovalori ....", a che osservatore ci si
riferisce? (Giorgio Grillini)
 All'osservatore identità la cui matrice dinamica è del tipo
(A + KC) essendo A e C rispettivamente la matrice dinamica e quella di
distribuzione delle uscite del sistema da osservare.
All'osservatore identità la cui matrice dinamica è del tipo
(A + KC) essendo A e C rispettivamente la matrice dinamica e quella di
distribuzione delle uscite del sistema da osservare.
 #59
Non sono riuscito a capire bene il calcolo della matrice di transizione,
ad esempio per il sistema con matrice dinamica #59
Non sono riuscito a capire bene il calcolo della matrice di transizione,
ad esempio per il sistema con matrice dinamica
| -d 1 0 |
A = | 0 -d 0 |
| 0 0 -e |
Mi potrebbe spiegare cortesemente i procedimenti di calcolo per un
sistema lineare stazionario continuo? (Fabio Marcantonini)
 La matrice di transizione è, in questo caso, l'esponenziale di matrice
e può venire calcolata con uno qualunque dei metodi che abbiamo visto
a lezione (e che può trovare descritti sul testo di teoria adottato)
per le funzioni di matrice. Può anche fare riferimento ai numerosi
esempi riportati sul testo Teoria dei sistemi: Esercizi e Applicazioni
(Esercizi 3,5,8,9,16,21,23 e 24).
Nelle esercitazioni svolte durante il corso abbiamo quasi sempre usato il
metodo del polinomio interpolante che richiede l'inversione della matrice di
Vandermonde associata agli autovalori della matrice di cui calcolare la
funzione; nel caso che lei sottopone tuttavia la matrice è in forma di
Jordan e la forma dell'esponenziale è nota (anche questa la può
trovare direttamente sul testo di teoria adottato) e può venire
quindi scritta senza la necessità di effettuare alcun calcolo. Risulta
infatti:
La matrice di transizione è, in questo caso, l'esponenziale di matrice
e può venire calcolata con uno qualunque dei metodi che abbiamo visto
a lezione (e che può trovare descritti sul testo di teoria adottato)
per le funzioni di matrice. Può anche fare riferimento ai numerosi
esempi riportati sul testo Teoria dei sistemi: Esercizi e Applicazioni
(Esercizi 3,5,8,9,16,21,23 e 24).
Nelle esercitazioni svolte durante il corso abbiamo quasi sempre usato il
metodo del polinomio interpolante che richiede l'inversione della matrice di
Vandermonde associata agli autovalori della matrice di cui calcolare la
funzione; nel caso che lei sottopone tuttavia la matrice è in forma di
Jordan e la forma dell'esponenziale è nota (anche questa la può
trovare direttamente sul testo di teoria adottato) e può venire
quindi scritta senza la necessità di effettuare alcun calcolo. Risulta
infatti:
| exp(-dt) t*exp(-dt) 0 |
exp(At) = | 0 exp(-dt) 0 |
| 0 0 exp(-et) |
 #60
Appena illustrata la nozione di osservabilità, a lezione lei ha spiegato
che nei sistemi lineari la determinazione dell'insieme caratteristico
E-(t0,t1,u(.),y(.)) non è legata
allo specifico ingresso, poiché esso coincide con
E-(t0,t1,0,y0(.)).
Effettivamente, per via della scomponibilità del moto in tali sistemi,
la risposta forzata è, per un dato ingresso, la stessa per tutti gli
stati dello spazio degli stati X e dunque ciò che distingue gli stati
è la loro risposta libera y0(.).
Se però i "dati" del problema dell'osservazione dello stato iniziale
sono le funzioni u(.) e y(.), l'estrazione della risposta libera
y0(.) dalla y(.) non può prescindere dalla u(.),
giacché, per ogni t>=t0,
y0(t) = y(t)-yf(t) = y(t)-gamma(t,t0,u(.),0).
Come possiamo allora dire che E-(t0,t1,u(.),y(.))
=E-(t0,t1,0,y0(.))
non dipende da u(.)?
(Paolo Gianessi) #60
Appena illustrata la nozione di osservabilità, a lezione lei ha spiegato
che nei sistemi lineari la determinazione dell'insieme caratteristico
E-(t0,t1,u(.),y(.)) non è legata
allo specifico ingresso, poiché esso coincide con
E-(t0,t1,0,y0(.)).
Effettivamente, per via della scomponibilità del moto in tali sistemi,
la risposta forzata è, per un dato ingresso, la stessa per tutti gli
stati dello spazio degli stati X e dunque ciò che distingue gli stati
è la loro risposta libera y0(.).
Se però i "dati" del problema dell'osservazione dello stato iniziale
sono le funzioni u(.) e y(.), l'estrazione della risposta libera
y0(.) dalla y(.) non può prescindere dalla u(.),
giacché, per ogni t>=t0,
y0(t) = y(t)-yf(t) = y(t)-gamma(t,t0,u(.),0).
Come possiamo allora dire che E-(t0,t1,u(.),y(.))
=E-(t0,t1,0,y0(.))
non dipende da u(.)?
(Paolo Gianessi)
 Per il semplice motivo che otteniamo lo stesso sottospazio qualunque sia
la funzione di ingresso applicata al sistema.
Per il semplice motivo che otteniamo lo stesso sottospazio qualunque sia
la funzione di ingresso applicata al sistema.
 #61
Con riferimento alle equazioni #61
Con riferimento alle equazioni
dx(t)/dt = A(t)x(t) (1)
dx(t)/dt = A(t)x(t) + B(t)u(t) (2)
che descrivono la velocità di transizione dello stato in un sistema dinamico
lineare nonstazionario nei casi libero e forzato, le pongo le seguenti domande:
a) Sappiamo che l'insieme delle soluzioni di (1) è uno spazio vettoriale V di
dimensione n (=dimensione dello spazio degli stati) una cui base è data da
un insieme di soluzioni di (1) linearmente indipendenti quali ad esempio
le colonne della matrice di transizione dello stato. Ma cosa vuol dire
"funzioni linearmente indipendenti"? Forse un insieme (fi(t))
i=1..n tale che
per ogni t i vettori fi(t) siano tra loro linearmente indipendenti?
b) Non mi è chiaro per quale motivo x(.) = 0, soluzione ovvia di (1), è
l'unica a potersi annullare, o meglio: per quale motivo per ogni x*(.)
soluzione di (1) vale l'implicazione: (esiste t*) t.c. x*(t*) = 0 =>
x*(.) è la soluzione ovvia?
c) Sviluppando la (1) si ha:
dx(t) = A(t)x(t)dt => x(t) = x(t0) + integrale di [A(tau)x(tau)dtau] da t0
a t, equivalente a x(t) = Phi(t,t0) x(t0).
Sviluppando in modo analogo la (2), si ottiene x(t) =
x(t0) + int.
di [A(tau)x(tau)dtau] da t0 a t + int. di [B(tau)u(tau)dtau] da t0
a t = Phi(t,t0)x(t0)
+ int. di [B(tau)u(tau)dtau], diversa dall'espressione fornita dal testo e
da lei a lezione, nella quale nell'ultimo integrale u(tau) è premoltiplicato
non per B(tau) ma per il nucleo di convoluzione V(t,tau). Dov'è che sbaglio?
d)Qual'è il significato fisico dei due nuclei di convoluzione
V(t,tau) := Phi(t,tau)B(tau), W(t,tau) := C(t)Phi(t,tau)B(tau)?
(Paolo Gianessi)
 a) Le funzioni fi(t) vengono definite linearmente indipendenti
quando nessuna di esse può venire espressa come combinazione lineare
delle rimanenti; si tratta, come vede, della usuale definizione di lineare
indipendenza.
a) Le funzioni fi(t) vengono definite linearmente indipendenti
quando nessuna di esse può venire espressa come combinazione lineare
delle rimanenti; si tratta, come vede, della usuale definizione di lineare
indipendenza.
b) La proprietà da lei citata è una conseguenza del teorema di
esistenza e unicità della soluzione di un'equazione differenziale
lineare che dovrebbe già conoscere per il caso scalare.
Per il caso vettoriale può fare riferimento alla dimostrazione riportata
sul testo di teoria adottato.
c) Nel non considerare correttamente l'azione dell'ingresso sullo stato
nell'integrazione di dx; può facilmente verificare la non correttezza
della espressione da lei ottenuta calcolandone la derivata.
d) Come ho sottolineato più volte, allo stato di un sistema non è
necessariamente associato un significato fisico; non è quindi possibile, in
generale, dare un significato fisico a V(t,tau).
Sul significato fisico di W(t,tau) (matrice di risposta impulsiva) mi sono
invece soffermato a lungo; la invito quindi a riguardare gli appunti presi
a lezione o la descrizione riportata sul libro di testo.
 #62
Vorrei un chiarimento riguardo alla relazione tra il polinomio minimo e la
parte raggiungibile e osservabile di un sistema. In particolare, perché l'ordine
della parte raggiungibile e osservabile di un sistema è uguale al grado del
polinomio minimo?
Inoltre, sussiste qualche relazione tra i poli di un sistema e gli zeri del polinomio
minimo? (Marco Bevilacqua) #62
Vorrei un chiarimento riguardo alla relazione tra il polinomio minimo e la
parte raggiungibile e osservabile di un sistema. In particolare, perché l'ordine
della parte raggiungibile e osservabile di un sistema è uguale al grado del
polinomio minimo?
Inoltre, sussiste qualche relazione tra i poli di un sistema e gli zeri del polinomio
minimo? (Marco Bevilacqua)
 Consideriamo la matrice di trasferimento del sistema che, come abbiamo verificato
facendo riferimento alla scomposizione canonica di Kalman, descrive la sola parte
raggiungibile ed osservabile del sistema. Risulta G(s)=C(sI-A)-1B=
C agg(sI-A)B/p(s) ove p(s)=det(sI-A) indica il polinomio caratteristico
di A. Se ora indichiamo con r(s) il massimo comun divisore monico degli elementi
di agg(sI-A) e ricordiamo la relazione m(s)=p(s)/r(s) ove m(s) indica il polinomio
minimo di A, arriviamo subito alla relazione G(s) = P(s)/m(s) (ove P(s)=agg(sI-A)/r(s))
che dimostra quanto da lei richiesto.
I poli di un sistema sono gli zeri dei polinomi a denominatore negli elementi della
matrice di trasferimento quindi, per quanto visto sopra, gli zeri del polinomio minimo
di A, cioè gli autovalori associati alla parte raggiungibile ed osservabile
del sistema.
Consideriamo la matrice di trasferimento del sistema che, come abbiamo verificato
facendo riferimento alla scomposizione canonica di Kalman, descrive la sola parte
raggiungibile ed osservabile del sistema. Risulta G(s)=C(sI-A)-1B=
C agg(sI-A)B/p(s) ove p(s)=det(sI-A) indica il polinomio caratteristico
di A. Se ora indichiamo con r(s) il massimo comun divisore monico degli elementi
di agg(sI-A) e ricordiamo la relazione m(s)=p(s)/r(s) ove m(s) indica il polinomio
minimo di A, arriviamo subito alla relazione G(s) = P(s)/m(s) (ove P(s)=agg(sI-A)/r(s))
che dimostra quanto da lei richiesto.
I poli di un sistema sono gli zeri dei polinomi a denominatore negli elementi della
matrice di trasferimento quindi, per quanto visto sopra, gli zeri del polinomio minimo
di A, cioè gli autovalori associati alla parte raggiungibile ed osservabile
del sistema.
 #63
In un sistema lineare stazionario a tempo continuo, il sottospazio di
raggiungibilità dello stato zero non dipende dall'ampiezza dell'intervallo
di tempo che si ha a disposizione; vorrei sapere se, considerando uno stato
diverso dallo stato zero, gli elementi di R+(x) cambiano in funzione
dell'intervallo di tempo. Si può supporre un'interpretazione per cui, se lo stato
x appartiene a
R+(0) allora gli elementi di R+(0) coincidono con quelli di
R+(0) mentre se x non appartiene a R+(0) il contributo del moto
libero fa variare gli elementi di R+(x) in funzione del tempo?
(Marco Bevilacqua) #63
In un sistema lineare stazionario a tempo continuo, il sottospazio di
raggiungibilità dello stato zero non dipende dall'ampiezza dell'intervallo
di tempo che si ha a disposizione; vorrei sapere se, considerando uno stato
diverso dallo stato zero, gli elementi di R+(x) cambiano in funzione
dell'intervallo di tempo. Si può supporre un'interpretazione per cui, se lo stato
x appartiene a
R+(0) allora gli elementi di R+(0) coincidono con quelli di
R+(0) mentre se x non appartiene a R+(0) il contributo del moto
libero fa variare gli elementi di R+(x) in funzione del tempo?
(Marco Bevilacqua)
 La notazione che lei utilizza non può venire considerata corretta perché
la notazione R+(x) fa implicitamente riferimento ad un intervallo di ampiezza
non limitata; andrebbe quindi aggiunto il pedice "t" all'insieme considerato per poterlo
riferire ad intervalli di ampiezza limitata. Ciò posto, le ricordo che l'insieme
Rt+(x) è la varietà lineare definita dal sottospazio
R+(0) e dallo stato eAtx. Tale insieme è quindi soggetto
a variazioni in funzione di t a meno che x non appartenga ad un sottospazio invariante
rispetto ad A contenuto in R+(0); un caso di rilievo che soddisfa questa
condizione è ovviamente costituito dalla condizione R+(0)=X.
La notazione che lei utilizza non può venire considerata corretta perché
la notazione R+(x) fa implicitamente riferimento ad un intervallo di ampiezza
non limitata; andrebbe quindi aggiunto il pedice "t" all'insieme considerato per poterlo
riferire ad intervalli di ampiezza limitata. Ciò posto, le ricordo che l'insieme
Rt+(x) è la varietà lineare definita dal sottospazio
R+(0) e dallo stato eAtx. Tale insieme è quindi soggetto
a variazioni in funzione di t a meno che x non appartenga ad un sottospazio invariante
rispetto ad A contenuto in R+(0); un caso di rilievo che soddisfa questa
condizione è ovviamente costituito dalla condizione R+(0)=X.
 #64
Il concetto di polo è stato introdotto nell'ambito dei modelli di ingresso/uscita
mentre talora mi pare che venga usato (anche sul libro dei test) in contesti più
ampi, e mi capita spesso in tali contesti di mescolare il significato di poli e
autovalori. (Luca Fiuzzi) #64
Il concetto di polo è stato introdotto nell'ambito dei modelli di ingresso/uscita
mentre talora mi pare che venga usato (anche sul libro dei test) in contesti più
ampi, e mi capita spesso in tali contesti di mescolare il significato di poli e
autovalori. (Luca Fiuzzi)
 I poli di un sistema sono gli zeri dei polinomi a denominatore negli elementi della
matrice di trasferimento; coincidono con gli zeri del polinomio minimo della matrice
dinamica del sistema o, se preferisce, con gli autovalori associati alla parte
raggiungibile ed osservabile del sistema. I poli quindi sono una parte degli autovalori
del sistema; per i sistemi completamente raggiungibili ed osservabili poli ed autovalori
della matrice dinamica coincidono e i due termini possono venire usati indifferentemente.
I poli di un sistema sono gli zeri dei polinomi a denominatore negli elementi della
matrice di trasferimento; coincidono con gli zeri del polinomio minimo della matrice
dinamica del sistema o, se preferisce, con gli autovalori associati alla parte
raggiungibile ed osservabile del sistema. I poli quindi sono una parte degli autovalori
del sistema; per i sistemi completamente raggiungibili ed osservabili poli ed autovalori
della matrice dinamica coincidono e i due termini possono venire usati indifferentemente.
 #65
Risposta armonica, nozioni di base. (Clementina D'Onofrio) #65
Risposta armonica, nozioni di base. (Clementina D'Onofrio)
 La risposta armonica o frequenziale descrive il comportamento a regime
di un sistema lineare quando al suo ingresso viene applicato un segnale
sinusoidale. Se si considera un sistema con un solo ingresso ed una sola uscita
e si indica con omega la pulsazione della sinusoide in ingresso e con G(s)
la funzione di trasferimento, la risposta frequenziale è data dalla
funzione G(j omega) il cui modulo fornisce il rapporto tra l'ampiezza della
sinusoide in uscita e quella di ingresso (ovviamente della stessa frequenza
data la linearità del sistema) mentre l'argomento fornisce lo
sfasamento tra le due sinusoidi. L'estensione al caso di più ingressi
ed uscite si ottiene considerando i singoli elementi della matrice di
trasferimento (cioè le funzioni di trasferimento tra i singoli ingressi
e le singole uscite); si ricordi inoltre che per i sistemi lineari vale la
sovrapposizione degli effetti.
La risposta armonica o frequenziale descrive il comportamento a regime
di un sistema lineare quando al suo ingresso viene applicato un segnale
sinusoidale. Se si considera un sistema con un solo ingresso ed una sola uscita
e si indica con omega la pulsazione della sinusoide in ingresso e con G(s)
la funzione di trasferimento, la risposta frequenziale è data dalla
funzione G(j omega) il cui modulo fornisce il rapporto tra l'ampiezza della
sinusoide in uscita e quella di ingresso (ovviamente della stessa frequenza
data la linearità del sistema) mentre l'argomento fornisce lo
sfasamento tra le due sinusoidi. L'estensione al caso di più ingressi
ed uscite si ottiene considerando i singoli elementi della matrice di
trasferimento (cioè le funzioni di trasferimento tra i singoli ingressi
e le singole uscite); si ricordi inoltre che per i sistemi lineari vale la
sovrapposizione degli effetti.
 #66
Una matrice di transizione FI(i,j), con i>j, per un sistema dinamico descritto
dal modello x(t+1)=B(t)u(t)
è sempre una matrice idempotente e nilpotente? (A=A*A=A*A*...*A=0) (R.R.) #66
Una matrice di transizione FI(i,j), con i>j, per un sistema dinamico descritto
dal modello x(t+1)=B(t)u(t)
è sempre una matrice idempotente e nilpotente? (A=A*A=A*A*...*A=0) (R.R.)
 Nel sistema da lei considerato risulta A=0 quindi valgono le proprietà da lei indicate.
Nel sistema da lei considerato risulta A=0 quindi valgono le proprietà da lei indicate.
 #67
Per quale motivo l'integrale di un impulso Dirac è uguale ad 1? Infatti l'impulso
Dirac corrisponde ad un "bastoncino" di base praticamente nulla ed altezza infinita
e quindi l'area sottesa da tale curva è nulla. Allora è forse una convenzione?
Inoltre per quale motivo l'integrale del prodotto di una funzione f(t) con l'impulso
di Dirac (applicato in t0) è uguale al valore che assume la funzione nel
punto t0? O meglio come si spiega (matematicamente) il fatto che effettuando
il prodotto, il "bastoncino" dell'impulso di Dirac non ha più altezza infinita, ma ha
altezza uguale all'"altezza" della funzione f"? (Luca Scalorbi) #67
Per quale motivo l'integrale di un impulso Dirac è uguale ad 1? Infatti l'impulso
Dirac corrisponde ad un "bastoncino" di base praticamente nulla ed altezza infinita
e quindi l'area sottesa da tale curva è nulla. Allora è forse una convenzione?
Inoltre per quale motivo l'integrale del prodotto di una funzione f(t) con l'impulso
di Dirac (applicato in t0) è uguale al valore che assume la funzione nel
punto t0? O meglio come si spiega (matematicamente) il fatto che effettuando
il prodotto, il "bastoncino" dell'impulso di Dirac non ha più altezza infinita, ma ha
altezza uguale all'"altezza" della funzione f"? (Luca Scalorbi)
 L'impulso di Dirac non è una funzione e richiede, per una corretta trattazione
matematica, l'uso delle distribuzioni. La risposta all'impulso di Dirac di
qualunque sistema reale è tuttavia approssimabile
con la precisione desiderata attraverso la risposta ad un impulso di ampiezza
sufficientemente stretta e di area unitaria. Nell'ambito del corso abbiamo
considerato come impulso di Dirac il limite cui tende un impulso di ampiezza finita
e di area unitaria quando si fa tendere tale ampiezza a zero e, per una funzione
di tale tipo, valgono entrambe le proprietà da lei indicate.
L'impulso di Dirac non è una funzione e richiede, per una corretta trattazione
matematica, l'uso delle distribuzioni. La risposta all'impulso di Dirac di
qualunque sistema reale è tuttavia approssimabile
con la precisione desiderata attraverso la risposta ad un impulso di ampiezza
sufficientemente stretta e di area unitaria. Nell'ambito del corso abbiamo
considerato come impulso di Dirac il limite cui tende un impulso di ampiezza finita
e di area unitaria quando si fa tendere tale ampiezza a zero e, per una funzione
di tale tipo, valgono entrambe le proprietà da lei indicate.
 #68
Un sistema dinamico lineare e stazionario, ridotto in forma minima,
ha al più due blocchi (i due blocchi osservabili)? Perché?
Vale anche per i sistemi discreti? (Sun Dec 12 15:36:56 1999, R.R.) #68
Un sistema dinamico lineare e stazionario, ridotto in forma minima,
ha al più due blocchi (i due blocchi osservabili)? Perché?
Vale anche per i sistemi discreti? (Sun Dec 12 15:36:56 1999, R.R.)
 Un sistema è in forma minima quando privo di stati equivalenti e questo
equivale, per i sistemi lineari stazionari continui e discreti, alla
completa osservabilità. Nella scomposizione canonica di Kalman di tali
sistemi potranno quindi essere presenti solamente blocchi relativi alle
parti osservabili.
Un sistema è in forma minima quando privo di stati equivalenti e questo
equivale, per i sistemi lineari stazionari continui e discreti, alla
completa osservabilità. Nella scomposizione canonica di Kalman di tali
sistemi potranno quindi essere presenti solamente blocchi relativi alle
parti osservabili.
 #69
Un sistema dinamico, lineare e stazionario, discreto, con un solo ingresso
ed una sola uscita ha il polinomio minimo della matrice dinamica diverso
dal polinomio caratteristico. È necessariamente asintoticamente stabile?
Perché? Tali caratteristiche del sistema, a quali proprietà, circa la
stabilità, possono essere legate? (Sun Dec 12 15:36:56 1999, R.R.) #69
Un sistema dinamico, lineare e stazionario, discreto, con un solo ingresso
ed una sola uscita ha il polinomio minimo della matrice dinamica diverso
dal polinomio caratteristico. È necessariamente asintoticamente stabile?
Perché? Tali caratteristiche del sistema, a quali proprietà, circa la
stabilità, possono essere legate? (Sun Dec 12 15:36:56 1999, R.R.)
 L'informazione deducibile dalla non coincidenza tra il polinomio minimo
e quello caratteristico riguarda la presenza, nella matrice dinamica del
sistema, di almeno due blocchi di Jordan associati allo stesso autovalore
e questo implica, nel caso da lei citato, che il sistema non sia né
completamente raggiungibile né completamente osservabile. Non vi è invece
alcuna connessione con la stabilità a meno di non aggiungere altre
informazioni (es. blocchi multipli associati ad un autovalore con
modulo unitario).
L'informazione deducibile dalla non coincidenza tra il polinomio minimo
e quello caratteristico riguarda la presenza, nella matrice dinamica del
sistema, di almeno due blocchi di Jordan associati allo stesso autovalore
e questo implica, nel caso da lei citato, che il sistema non sia né
completamente raggiungibile né completamente osservabile. Non vi è invece
alcuna connessione con la stabilità a meno di non aggiungere altre
informazioni (es. blocchi multipli associati ad un autovalore con
modulo unitario).
 #70
Per un sistema dinamico a tempo discreto x(k+1)=Ax(k)+Bu(k), di ordine
n, risulta im B = n e dim KerC > 0.
La condizione dim KerC > 0 indica che lo spazio nullo della matrice C
ha dimensione maggiore o uguale ad 1.
Perché ciò è compatibile con la completa osservabilità del sistema?
(Sun Dec 19 17:25:52 1999, R.R.) #70
Per un sistema dinamico a tempo discreto x(k+1)=Ax(k)+Bu(k), di ordine
n, risulta im B = n e dim KerC > 0.
La condizione dim KerC > 0 indica che lo spazio nullo della matrice C
ha dimensione maggiore o uguale ad 1.
Perché ciò è compatibile con la completa osservabilità del sistema?
(Sun Dec 19 17:25:52 1999, R.R.)
 La condizione dim KerC > 0 implica solo che non si possa ricostruire
direttamente lo stato dall'uscita mediante la relazione algebrica
x(t) = P+y(t). L'osservatore dello stato è invece un sistema
dinamico cioè dotato di memoria in grado di ricostruire lo stato in base
alla osservazione di un certo numero di campioni dell'ingresso e dell'uscita
del sistema. In altre parole, l'informazione sullo stato al tempo t che non viene
fornita dall'uscita in tale istante viene dedotta dai valori che l'uscita
assume in altri istanti.
La condizione dim KerC > 0 implica solo che non si possa ricostruire
direttamente lo stato dall'uscita mediante la relazione algebrica
x(t) = P+y(t). L'osservatore dello stato è invece un sistema
dinamico cioè dotato di memoria in grado di ricostruire lo stato in base
alla osservazione di un certo numero di campioni dell'ingresso e dell'uscita
del sistema. In altre parole, l'informazione sullo stato al tempo t che non viene
fornita dall'uscita in tale istante viene dedotta dai valori che l'uscita
assume in altri istanti.
 #71
Un sistema dinamico, lineare e stazionario, risulta stabile i.l.u.l, ma non i.l.s.l.
Ciò vuol dire che esistono modi semplicemente stabili o instabli nella parte raggiungibile
e non osservabile del sistema.
Non possiamo dire nulla sulla completa raggiungibilità del sistema, dal momento che non
sappiamo se esiste una parte osservabile e non raggiungibile?
(Sun Dec 19 17:25:52 1999, R.R.) #71
Un sistema dinamico, lineare e stazionario, risulta stabile i.l.u.l, ma non i.l.s.l.
Ciò vuol dire che esistono modi semplicemente stabili o instabli nella parte raggiungibile
e non osservabile del sistema.
Non possiamo dire nulla sulla completa raggiungibilità del sistema, dal momento che non
sappiamo se esiste una parte osservabile e non raggiungibile?
(Sun Dec 19 17:25:52 1999, R.R.)
 Certamente
Certamente
 #72
Per quali tipi di sistemi la completa ossevabilità implica la completa ricostruibilità?
E per quali la completa raggiungibilità implica la completa controllabilità?
(Considerare il caso sia di sistemi continui, sia discreti). (Sun Dec 19 17:25:52 1999, R.R.) #72
Per quali tipi di sistemi la completa ossevabilità implica la completa ricostruibilità?
E per quali la completa raggiungibilità implica la completa controllabilità?
(Considerare il caso sia di sistemi continui, sia discreti). (Sun Dec 19 17:25:52 1999, R.R.)
 Le implicazioni da lei considerate derivano dalla non singolarità della matrice di transizione;
sono quindi sempre vere per i sistemi continui e per quelli discreti con matrice di
transizione non singolare come, ad esempio, i modelli discreti dei sistemi continui.
Le implicazioni da lei considerate derivano dalla non singolarità della matrice di transizione;
sono quindi sempre vere per i sistemi continui e per quelli discreti con matrice di
transizione non singolare come, ad esempio, i modelli discreti dei sistemi continui.
 #73
Un sistema puramente dinamico, con un ingresso ed una uscita ed n autovalori
distinti, ha il polinomio minimo uguale al polinomio caratteristico, indipendentemente
dalla sua completa raggiungibilità e osservabilità. La funzione di trasferimento
G(s) ha come denominatore il polinomio minimo della matrice dinamica associata
alla parte raggiungibile ed osservabile. Il grado del denominatore è sempre uguale
ad n sia che il sistema sia completamente raggiungibile ed osservabile che in caso
contrario, essendo tutti gli autovalori distinti? (Sun Dec 19 17:25:52 1999, R.R.) #73
Un sistema puramente dinamico, con un ingresso ed una uscita ed n autovalori
distinti, ha il polinomio minimo uguale al polinomio caratteristico, indipendentemente
dalla sua completa raggiungibilità e osservabilità. La funzione di trasferimento
G(s) ha come denominatore il polinomio minimo della matrice dinamica associata
alla parte raggiungibile ed osservabile. Il grado del denominatore è sempre uguale
ad n sia che il sistema sia completamente raggiungibile ed osservabile che in caso
contrario, essendo tutti gli autovalori distinti? (Sun Dec 19 17:25:52 1999, R.R.)
 Il grado dei polinomi a denominatore negli elementi della matrice razionale
(sI-A)-1 è uguale, in questo caso, ad n data la coincidenza tra
polinomio minimo e caratteristico (il massimo comun divisore monico della matrice
polinomiale agg(sI-A) è di grado zero cioè uguale ad 1).
Il grado del denominatore della funzione di trasferimento è invece uguale alla
dimensione della parte raggiungibile ed osservabile del sistema che può benissimo
non coincidere con l'intero sistema; lo può immediatamente verificare su un sistema
di ordine n con autovalori tutti distinti e B=[1 0 ... 0]T,
C=[1 0 ... 0].
Il grado dei polinomi a denominatore negli elementi della matrice razionale
(sI-A)-1 è uguale, in questo caso, ad n data la coincidenza tra
polinomio minimo e caratteristico (il massimo comun divisore monico della matrice
polinomiale agg(sI-A) è di grado zero cioè uguale ad 1).
Il grado del denominatore della funzione di trasferimento è invece uguale alla
dimensione della parte raggiungibile ed osservabile del sistema che può benissimo
non coincidere con l'intero sistema; lo può immediatamente verificare su un sistema
di ordine n con autovalori tutti distinti e B=[1 0 ... 0]T,
C=[1 0 ... 0].
 #74
Se la funzione di trasferimento di un sistema, con un ingresso ed una uscita, è il
rapporto di due polinomi dello stesso ordine, il sistema è puramente algebrico.
Perché posso dire che il sistema è dinamico, non puramente?
(Sun Dec 19 17:25:52 1999, R.R.) #74
Se la funzione di trasferimento di un sistema, con un ingresso ed una uscita, è il
rapporto di due polinomi dello stesso ordine, il sistema è puramente algebrico.
Perché posso dire che il sistema è dinamico, non puramente?
(Sun Dec 19 17:25:52 1999, R.R.)
 Il sistema considerato non è affatto "puramente algebrico". È invece
non puramente dinamico che è tutt'altra cosa. Un sistema non puramente
dinamico è un sistema dinamico nel quale l'ingresso agisce sull'uscita, oltre
che attraverso l'evoluzione dello stato come in tutti i sistemi dinamici,
anche in maniera diretta cioè attraverso un legame algebrico tra ingresso
ed uscita. Se considera, per maggior chiarezza, un modello a tempo discreto, si renderà
conto immediatamente che questo significa avere polinomi a denominatore e
numeratore della funzione di trasferimento dello stesso ordine. Riveda anche gli
esempi relativi a reti elettriche che ho utilizzato a lezione per illustrare
la differenza tra sistemi puramente dinamici e non.
Il sistema considerato non è affatto "puramente algebrico". È invece
non puramente dinamico che è tutt'altra cosa. Un sistema non puramente
dinamico è un sistema dinamico nel quale l'ingresso agisce sull'uscita, oltre
che attraverso l'evoluzione dello stato come in tutti i sistemi dinamici,
anche in maniera diretta cioè attraverso un legame algebrico tra ingresso
ed uscita. Se considera, per maggior chiarezza, un modello a tempo discreto, si renderà
conto immediatamente che questo significa avere polinomi a denominatore e
numeratore della funzione di trasferimento dello stesso ordine. Riveda anche gli
esempi relativi a reti elettriche che ho utilizzato a lezione per illustrare
la differenza tra sistemi puramente dinamici e non.
 #75
Due sistemi dinamici, lineari e stazionari, completamente raggiungibili, hanno matrici
di risposta impulsiva coincidenti. Possono avere matrici dinamiche simili? Perché?
(Sun Dec 19 17:25:52 1999, R.R.) #75
Due sistemi dinamici, lineari e stazionari, completamente raggiungibili, hanno matrici
di risposta impulsiva coincidenti. Possono avere matrici dinamiche simili? Perché?
(Sun Dec 19 17:25:52 1999, R.R.)
 La coincidenza delle matrici di risposta impulsiva implica la similitudine delle
matrici dinamiche della parte raggiungibile ed osservabile dei due sistemi mentre
non fornisce alcuna informazione sulle parti restanti.
La coincidenza delle matrici di risposta impulsiva implica la similitudine delle
matrici dinamiche della parte raggiungibile ed osservabile dei due sistemi mentre
non fornisce alcuna informazione sulle parti restanti.
 #76
In un sistema dinamico, lineare e stazionario, in forma minima e completamente raggiungibile,
la stabilità ilsl coincide con la stabilità ilul? Sono entrambe uguali alla stabilità asintotica?
Perché? (Sun Dec 19 17:25:52 1999, R.R.) #76
In un sistema dinamico, lineare e stazionario, in forma minima e completamente raggiungibile,
la stabilità ilsl coincide con la stabilità ilul? Sono entrambe uguali alla stabilità asintotica?
Perché? (Sun Dec 19 17:25:52 1999, R.R.)
 In un sistema di questo tipo esiste solo la parte completamente raggiungibile ed osservabile
quindi le condizioni relative ai tre tipi di stabilità sono necessariamente coincidenti.
In un sistema di questo tipo esiste solo la parte completamente raggiungibile ed osservabile
quindi le condizioni relative ai tre tipi di stabilità sono necessariamente coincidenti.
 #77
Perché nei sistemi dinamici, lineari e stazionari, stabili ilsl, gli elementi della matrici
di risposta impulsiva sono funzioni che tendono a zero al tendere del tempo all infinito?
(Sun Dec 19 17:25:52 1999, R.R.) #77
Perché nei sistemi dinamici, lineari e stazionari, stabili ilsl, gli elementi della matrici
di risposta impulsiva sono funzioni che tendono a zero al tendere del tempo all infinito?
(Sun Dec 19 17:25:52 1999, R.R.)
 Perché combinazioni di modi della parte raggiungibile ed osservabile che, nei sistemi stabili
ilsl, sono asintoticamente stabili. Tenga presente che la stessa proprietà vale anche per
i sistemi stabili ilul e, ovviamente, per quelli asintoticamente stabili.
Perché combinazioni di modi della parte raggiungibile ed osservabile che, nei sistemi stabili
ilsl, sono asintoticamente stabili. Tenga presente che la stessa proprietà vale anche per
i sistemi stabili ilul e, ovviamente, per quelli asintoticamente stabili.
 #78
Quali caratterisiche ha l'errore di stima dello stato in un osservatore identità per un sistema
dinamico, lineare e stazionario, non in forma minima? (Sun Dec 19 17:25:52 1999, R.R.) #78
Quali caratterisiche ha l'errore di stima dello stato in un osservatore identità per un sistema
dinamico, lineare e stazionario, non in forma minima? (Sun Dec 19 17:25:52 1999, R.R.)
 La dinamica dell'errore associato allo stato della parte osservabile del sistema può
venire assegnata ad arbitrio scegliendo opportunamente la matrice dei guadagni dell'osservatore;
quella dell'errore associato alla stima dello stato della parte non osservabile coincide invece
con la dinamica di tale parte del sistema (quindi tale errore tende a zero al crescere del tempo
solo se la parte non osservabile del sistema risulta asintoticamente stabile).
La dinamica dell'errore associato allo stato della parte osservabile del sistema può
venire assegnata ad arbitrio scegliendo opportunamente la matrice dei guadagni dell'osservatore;
quella dell'errore associato alla stima dello stato della parte non osservabile coincide invece
con la dinamica di tale parte del sistema (quindi tale errore tende a zero al crescere del tempo
solo se la parte non osservabile del sistema risulta asintoticamente stabile).
 #79
Non mi è chiaro perché in un sistema lineare e stazionario E+t1(0,0) sia contenuto in
E+t2(0,0) se t2>t1. Potrebbe rispiegarmelo. (Sun Jan 2 23:10:58 2000, Alessandro Caselli) #79
Non mi è chiaro perché in un sistema lineare e stazionario E+t1(0,0) sia contenuto in
E+t2(0,0) se t2>t1. Potrebbe rispiegarmelo. (Sun Jan 2 23:10:58 2000, Alessandro Caselli)
 Ogni stato iniziale che, con ingresso nullo, generi uscita nulla in un certo intervallo di tempo genera la
stessa uscita nulla in qualunque sottointervallo indipendentemente, inoltre, dalla allocazione di tali
intervalli sull'asse dei tempi grazie alla ipotesi di stazionarietà.
Ogni stato iniziale che, con ingresso nullo, generi uscita nulla in un certo intervallo di tempo genera la
stessa uscita nulla in qualunque sottointervallo indipendentemente, inoltre, dalla allocazione di tali
intervalli sull'asse dei tempi grazie alla ipotesi di stazionarietà.
 #80
Ho scritto (più volte per la verità...) che x(t)=Teta(t)*Teta-1(t0).
Non si dovrebbe invece indicare, visto che abbiamo detto che la matrice di transizione
può essere espressa come prodotto di una certa matrice Teta funzione di t e della sua
inversa funzione di t0, x(t)=Teta(t)*Teta-1(t0)x0?
(Mon 27 Dec 22:32:19 1999, Raffaele Landolfi) #80
Ho scritto (più volte per la verità...) che x(t)=Teta(t)*Teta-1(t0).
Non si dovrebbe invece indicare, visto che abbiamo detto che la matrice di transizione
può essere espressa come prodotto di una certa matrice Teta funzione di t e della sua
inversa funzione di t0, x(t)=Teta(t)*Teta-1(t0)x0?
(Mon 27 Dec 22:32:19 1999, Raffaele Landolfi)
 La scomposizione della matrice di transizione non può inglobare in alcun modo lo stato iniziale
del sistema; lo stato iniziale deve quindi venire sempre incluso nella espressione del moto libero di
un sistema.
La scomposizione della matrice di transizione non può inglobare in alcun modo lo stato iniziale
del sistema; lo stato iniziale deve quindi venire sempre incluso nella espressione del moto libero di
un sistema.
 #81
A lezione abbiamo visto che se un sistema è lineare ed è diagnosticabile o incasellabile
allora è anche rispettivamente completamente osservabile o completamente ricostruibile.
Vale una proprietà analoga anche per quanto riguarda la controllabilità e la
raggiungibilità? (Sun Jan 2 23:14:28 2000, Alessandro Caselli) #81
A lezione abbiamo visto che se un sistema è lineare ed è diagnosticabile o incasellabile
allora è anche rispettivamente completamente osservabile o completamente ricostruibile.
Vale una proprietà analoga anche per quanto riguarda la controllabilità e la
raggiungibilità? (Sun Jan 2 23:14:28 2000, Alessandro Caselli)
 Solo indirettamente, attraverso il sistema duale. Le proprietà di raggiungibilità e di
controllabilità di un sistema corrispondono infatti a quelle di osservabilità e di
ricostruibilità del sistema duale.
Solo indirettamente, attraverso il sistema duale. Le proprietà di raggiungibilità e di
controllabilità di un sistema corrispondono infatti a quelle di osservabilità e di
ricostruibilità del sistema duale.
 #82
Sul testo di teoria, nel teorema sull'assegnabilità degli autovalori
si parla di sistema "controllabile" mentre a lezione abbiamo richiesto che fosse
"completamente raggiungibile": è la stessa cosa?
(Sun Jan 2 23:14:28 2000, Alessandro Caselli) #82
Sul testo di teoria, nel teorema sull'assegnabilità degli autovalori
si parla di sistema "controllabile" mentre a lezione abbiamo richiesto che fosse
"completamente raggiungibile": è la stessa cosa?
(Sun Jan 2 23:14:28 2000, Alessandro Caselli)
 La proprietà richiesta è la completa raggiungibilità che, per i sistemi continui e
per i modelli discreti dei sistemi continui coincide con la completa controllabilità,
spesso indicata sinteticamente come "controllabilità" come avviene nel punto
da lei citato del testo. Se si desidera tuttavia considerare il problema da un punto
di vista del tutto generale occorre considerare la completa raggiungibilità come
può facilmente verificare facendo riferimento alla scomposizione canonica di Kalman.
La proprietà richiesta è la completa raggiungibilità che, per i sistemi continui e
per i modelli discreti dei sistemi continui coincide con la completa controllabilità,
spesso indicata sinteticamente come "controllabilità" come avviene nel punto
da lei citato del testo. Se si desidera tuttavia considerare il problema da un punto
di vista del tutto generale occorre considerare la completa raggiungibilità come
può facilmente verificare facendo riferimento alla scomposizione canonica di Kalman.
 #83
In un sistema lineare stazionario discreto, in una lezione ho scritto che gli stati
controllabili allo stato zero sono uguali a Im(Ad)-1Pi
mentre sul libro viene usata l'espressione (Ad)-1ImPi.
Le due espressioni sono uguali o quale delle due è corretta?
Inoltre se Ad non è invertibile, come effettuo il calcolo?
(Mon Jan 3 18:50:31 2000, Simone Melchiori) #83
In un sistema lineare stazionario discreto, in una lezione ho scritto che gli stati
controllabili allo stato zero sono uguali a Im(Ad)-1Pi
mentre sul libro viene usata l'espressione (Ad)-1ImPi.
Le due espressioni sono uguali o quale delle due è corretta?
Inoltre se Ad non è invertibile, come effettuo il calcolo?
(Mon Jan 3 18:50:31 2000, Simone Melchiori)
 Si narra che il filosofo Benedetto Croce abbia risposto una volta ad un giornalista che
gli chiedeva come mai i filosofi rispondessero così spesso alle domande con altre
domande, con uno spiritoso "E perché no?". Le cito questo aneddoto perché sarei tentato
di rispondere alla sua domanda con la domanda seguente: Lei come calcola l'espressione
(Ad)-1Im(Pi) riportata sul testo?
La risposta, ovviamente, è che l'espressione che vi ho dato evidenzia proprio come
si procede al calcolo della espressione (del tutto equivalente) riportata nel testo.
Le ricordo poi che nella espressione considerata (Ad)-1
non indica, in generale, l'inversa di Ad ma l'immagine inversa
rispetto alla trasformazione lineare descritta da Ad; solo nel caso
Ad risulti non singolare tale trasformazione sarà descritta dalla
matrice inversa mentre negli altri casi si utilizzerà l'espressione che abbiamo
visto a lezione cioé (Ad)+(Im(Pi) int
Im(Ad)) + ker(A).
Si narra che il filosofo Benedetto Croce abbia risposto una volta ad un giornalista che
gli chiedeva come mai i filosofi rispondessero così spesso alle domande con altre
domande, con uno spiritoso "E perché no?". Le cito questo aneddoto perché sarei tentato
di rispondere alla sua domanda con la domanda seguente: Lei come calcola l'espressione
(Ad)-1Im(Pi) riportata sul testo?
La risposta, ovviamente, è che l'espressione che vi ho dato evidenzia proprio come
si procede al calcolo della espressione (del tutto equivalente) riportata nel testo.
Le ricordo poi che nella espressione considerata (Ad)-1
non indica, in generale, l'inversa di Ad ma l'immagine inversa
rispetto alla trasformazione lineare descritta da Ad; solo nel caso
Ad risulti non singolare tale trasformazione sarà descritta dalla
matrice inversa mentre negli altri casi si utilizzerà l'espressione che abbiamo
visto a lezione cioé (Ad)+(Im(Pi) int
Im(Ad)) + ker(A).
 #84
In un osservatore identità tra gli appunti ho scritto che se il sistema non è
completamente osservabile, posso modificare solo gli autovalori della parte osservabile,
mentre per le altre componenti seguirà la dinamica dei blocchi 3 e 4 della scomposizione
di Kalman. Studiando però mi sembrerebbe corretto che le componenti non osservabili
seguano la dinamica dei blocchi 1 e 3 della scomposizione di Kalman, che sono quelli
relativi appunto alla parte non osservabile. Hanno ragione i miei appunti o ho ragione io?
(Mon Jan 3 18:54:20 2000, Simone Melchiori) #84
In un osservatore identità tra gli appunti ho scritto che se il sistema non è
completamente osservabile, posso modificare solo gli autovalori della parte osservabile,
mentre per le altre componenti seguirà la dinamica dei blocchi 3 e 4 della scomposizione
di Kalman. Studiando però mi sembrerebbe corretto che le componenti non osservabili
seguano la dinamica dei blocchi 1 e 3 della scomposizione di Kalman, che sono quelli
relativi appunto alla parte non osservabile. Hanno ragione i miei appunti o ho ragione io?
(Mon Jan 3 18:54:20 2000, Simone Melchiori)
 L'osservatore di un sistema dinamico non ha mai parti non osservabili dato che la sua
uscita coincide con lo stato; lei intende, probabilmente, fare riferimento alla dinamica
di quella parte dell'osservatore preposta alla ricostruzione dello stato delle parti non
osservabili del sistema. La dinamica di tale parte
è la stessa della parte non osservabile del sistema (non è influenzata dalla
matrice K) quindi perché l'osservatore funzioni correttamente (come modello, per
quanto riguarda questa parte) è
necessario che le parti non osservabili del sistema (blocchi 1 e 3) abbiano tutti i modi
asintoticamente stabili. La dinamica della parte dell'osservatore preposta alla
ricostruzione (non dimentichiamo che il nome osservatore è improprio) dello
stato della parte osservabile del sistema (blocchi 2 e 4) può invece venire sempre
assegnata ad arbitrio agendo sulla matrice dei guadagni K.
Aggiungo una osservazione non specifica: a giudicare da tutto quello che avete
scritto negli appunti presi a lezione si deduce l'impressione che, a lezione,
anziché prendere appunti sarebbe meglio cercare di capire quanto il docente
espone. Questa sarebbe infatti la base migliore per affrontare lo studio degli
argomenti su base non mnemonica utilizzando il libro di testo e tutte le altre
sorgenti (tante per questo corso!) messe a disposizione invece che cercando di
dare un senso ad appunti spesso errati per la fretta e/o la mancata comprensione
di quanto si sta affannosamente scrivendo. Il prof. Giuseppe
Zwirner, che ho avuto l'onore di avere come docente, vietava tassativamente
che si prendessero appunti durante le sue lezioni proprio perché, la sua grande
esperienza didattica gli indicava chiaramente come ciò significasse perdere buona
parte della utilità della lezione stessa.
L'osservatore di un sistema dinamico non ha mai parti non osservabili dato che la sua
uscita coincide con lo stato; lei intende, probabilmente, fare riferimento alla dinamica
di quella parte dell'osservatore preposta alla ricostruzione dello stato delle parti non
osservabili del sistema. La dinamica di tale parte
è la stessa della parte non osservabile del sistema (non è influenzata dalla
matrice K) quindi perché l'osservatore funzioni correttamente (come modello, per
quanto riguarda questa parte) è
necessario che le parti non osservabili del sistema (blocchi 1 e 3) abbiano tutti i modi
asintoticamente stabili. La dinamica della parte dell'osservatore preposta alla
ricostruzione (non dimentichiamo che il nome osservatore è improprio) dello
stato della parte osservabile del sistema (blocchi 2 e 4) può invece venire sempre
assegnata ad arbitrio agendo sulla matrice dei guadagni K.
Aggiungo una osservazione non specifica: a giudicare da tutto quello che avete
scritto negli appunti presi a lezione si deduce l'impressione che, a lezione,
anziché prendere appunti sarebbe meglio cercare di capire quanto il docente
espone. Questa sarebbe infatti la base migliore per affrontare lo studio degli
argomenti su base non mnemonica utilizzando il libro di testo e tutte le altre
sorgenti (tante per questo corso!) messe a disposizione invece che cercando di
dare un senso ad appunti spesso errati per la fretta e/o la mancata comprensione
di quanto si sta affannosamente scrivendo. Il prof. Giuseppe
Zwirner, che ho avuto l'onore di avere come docente, vietava tassativamente
che si prendessero appunti durante le sue lezioni proprio perché, la sua grande
esperienza didattica gli indicava chiaramente come ciò significasse perdere buona
parte della utilità della lezione stessa.
 #85
In riferimento alla terza domanda dell'esercizio d'esame MT1 (modello termico di un transistore) volevo chiedere:
una volta calcolata la risposta frequenziale G(jw) è giusto rispondere alla domanda calcolando la y(t) come
y(t)=G(jw)*sin(sqrt(ad)t)? Agendo in questo modo ho trovata una risposta ancora sinusoidale e con la stessa
pulsazione della sinusoide in ingresso (come mi aspettavo) e con un'ampiezza differente: è questa ampiezza la
risposta al quesito del compito ? (Jan 4 08:41:40 2000, Gianluca Lucente) #85
In riferimento alla terza domanda dell'esercizio d'esame MT1 (modello termico di un transistore) volevo chiedere:
una volta calcolata la risposta frequenziale G(jw) è giusto rispondere alla domanda calcolando la y(t) come
y(t)=G(jw)*sin(sqrt(ad)t)? Agendo in questo modo ho trovata una risposta ancora sinusoidale e con la stessa
pulsazione della sinusoide in ingresso (come mi aspettavo) e con un'ampiezza differente: è questa ampiezza la
risposta al quesito del compito ? (Jan 4 08:41:40 2000, Gianluca Lucente)
 Il modulo della risposta frequenziale fornisce, per ogni pulsazione, il rapporto tra l'ampiezza a regime
della sinusoide in uscita e quella in ingresso mentre il suo argomento ci fornisce lo sfasamento tra
tali sinusoidi. Per rispondere alla domanda dell'esercizio da lei citato occorre dunque sostituire ad
w il valore sqrt(ad) e calcolare il modulo di G(jw). Il procedimento da lei
indicato non è corretto e mescola il dominio dei tempi con quello delle frequenze.
Il modulo della risposta frequenziale fornisce, per ogni pulsazione, il rapporto tra l'ampiezza a regime
della sinusoide in uscita e quella in ingresso mentre il suo argomento ci fornisce lo sfasamento tra
tali sinusoidi. Per rispondere alla domanda dell'esercizio da lei citato occorre dunque sostituire ad
w il valore sqrt(ad) e calcolare il modulo di G(jw). Il procedimento da lei
indicato non è corretto e mescola il dominio dei tempi con quello delle frequenze.
 #86
Ho svolto l'esercizio di realizzazione presente sul server riguardante i sistemi non puramente dinamici e
sono riuscito, con un sitema di ordine 1, a ricavare il modello nello spazio degli stati abbastanza faticosamente.
Qual è il metodo sistematico per procedere in questi casi ? (Jan 4 08:41:40 2000, Gianluca Lucente) #86
Ho svolto l'esercizio di realizzazione presente sul server riguardante i sistemi non puramente dinamici e
sono riuscito, con un sitema di ordine 1, a ricavare il modello nello spazio degli stati abbastanza faticosamente.
Qual è il metodo sistematico per procedere in questi casi ? (Jan 4 08:41:40 2000, Gianluca Lucente)
 Una volta ottenuto, con i procedimenti che abbiamo visto a lezione, un modello polinomiale di ingresso-uscita
dai dati osservati, la deduzione di un modello nello spazio degli stati completamente osservabile è molto
semplice. Può trovare tutta la procedura nell'esercizio 29 del testo Teoria dei Sistemi: Esercizi e
Applicazioni.
Una volta ottenuto, con i procedimenti che abbiamo visto a lezione, un modello polinomiale di ingresso-uscita
dai dati osservati, la deduzione di un modello nello spazio degli stati completamente osservabile è molto
semplice. Può trovare tutta la procedura nell'esercizio 29 del testo Teoria dei Sistemi: Esercizi e
Applicazioni.
 #87
Riguardo all'esercizio presente sul server CR1 (trasformatore di isolamento), si chiede di calcolare 2 modelli
nello spazio degli stati: uno con uscita la corrente assorbita dal generatore, l'altro con uscita la tensione
ai capi del carico. Considerando come corrente assorbita la i1 indicata in figura, ho
scritto C'=[1 1], mentre nel secondo caso ho trovato C"=[0 RL]. È tutto corretto?
(Tue Jan 4 08:42:34 2000, Gianluca Lucente) #87
Riguardo all'esercizio presente sul server CR1 (trasformatore di isolamento), si chiede di calcolare 2 modelli
nello spazio degli stati: uno con uscita la corrente assorbita dal generatore, l'altro con uscita la tensione
ai capi del carico. Considerando come corrente assorbita la i1 indicata in figura, ho
scritto C'=[1 1], mentre nel secondo caso ho trovato C"=[0 RL]. È tutto corretto?
(Tue Jan 4 08:42:34 2000, Gianluca Lucente)
 Sì.
Sì.
 #88
Non mi sono ben chiare le definizioni di stato zero e uscita zero. Lo stato zero è lo stato
x=0 (origine dello spazio degli stati) che risulta essere di equilibrio con ingresso
u=0 o con un qualunque ingresso? E l'uscita zero? (Tue Jan 4 10:02:17 2000, Claudio Beltrani) #88
Non mi sono ben chiare le definizioni di stato zero e uscita zero. Lo stato zero è lo stato
x=0 (origine dello spazio degli stati) che risulta essere di equilibrio con ingresso
u=0 o con un qualunque ingresso? E l'uscita zero? (Tue Jan 4 10:02:17 2000, Claudio Beltrani)
 Lo stato zero e l'uscita zero (vettore zero dello spazio degli stati e di quello delle uscite) esistono
solo per i sistemi a stato vettore ma hanno interesse solo per quelli lineari (continui o discreti).
Per tali sistemi è immediato verificare come lo stato zero sia di equilibrio con ingresso zero
e come generi, se il sistema è puramente dinamico, uscita nulla. Una ulteriore proprietà dello stato
zero nei sistemi lineari è quella di risultare equivalente ad ogni stato non osservabile; un sistema
lineare è quindi in forma minima quando nel suo insieme degli stati non sono presenti stati
equivalenti allo stato zero.
Lo stato zero e l'uscita zero (vettore zero dello spazio degli stati e di quello delle uscite) esistono
solo per i sistemi a stato vettore ma hanno interesse solo per quelli lineari (continui o discreti).
Per tali sistemi è immediato verificare come lo stato zero sia di equilibrio con ingresso zero
e come generi, se il sistema è puramente dinamico, uscita nulla. Una ulteriore proprietà dello stato
zero nei sistemi lineari è quella di risultare equivalente ad ogni stato non osservabile; un sistema
lineare è quindi in forma minima quando nel suo insieme degli stati non sono presenti stati
equivalenti allo stato zero.
 #89
Per un sistema discreto del primo ordine, lineare e stazionario, la risposta impulsiva vale
w(k)=cak-1b?
(Wed Jan 5 10:50:40 2000, R.R.) #89
Per un sistema discreto del primo ordine, lineare e stazionario, la risposta impulsiva vale
w(k)=cak-1b?
(Wed Jan 5 10:50:40 2000, R.R.)
 Certamente.
Certamente.
 #90
Il sistema x(k+1)=u(k), y(k)=x(k) è completamente osservabile e raggiungibile. Allora è sicuramente ricostruibile,
ma è completamente controllabile solo se A è non singolare. Essendo A=0, non possiamo dire nulla circa la controllabilità.
Vero? Perché? (Wed Jan 5 10:50:40 2000, R.R.) #90
Il sistema x(k+1)=u(k), y(k)=x(k) è completamente osservabile e raggiungibile. Allora è sicuramente ricostruibile,
ma è completamente controllabile solo se A è non singolare. Essendo A=0, non possiamo dire nulla circa la controllabilità.
Vero? Perché? (Wed Jan 5 10:50:40 2000, R.R.)
 Falso. Il sistema in esame è completamente controllabile; basta infatti applicare, in qualunque stato si trovi,
ingresso nullo per portare a zero lo stato in una sola transizione. Può ottenere lo stesso risultato calcolando
il sottospazio di controllabilità. Occorre al riguardo calcolare l'immagine inversa secondo A del sottospazio
di raggiungibilità; tale immagine inversa include il nucleo di A quindi coincide, in questo caso, con l'intero
spazio degli stati.
Falso. Il sistema in esame è completamente controllabile; basta infatti applicare, in qualunque stato si trovi,
ingresso nullo per portare a zero lo stato in una sola transizione. Può ottenere lo stesso risultato calcolando
il sottospazio di controllabilità. Occorre al riguardo calcolare l'immagine inversa secondo A del sottospazio
di raggiungibilità; tale immagine inversa include il nucleo di A quindi coincide, in questo caso, con l'intero
spazio degli stati.
 #91
Se dim ker C > 0, significa che E-(0,0) contiene più di un elemento. Allora il sistema non è
completamente osservabile. Dove sbaglio? (Wed Jan 5 10:50:40 2000, R.R.) #91
Se dim ker C > 0, significa che E-(0,0) contiene più di un elemento. Allora il sistema non è
completamente osservabile. Dove sbaglio? (Wed Jan 5 10:50:40 2000, R.R.)
 Sbaglia nel legare il sottospazio di inosservabilità al nucleo della matrice di distribuzione delle uscite;
E-(0,0) può benissimo contenere il solo vettore 0 anche quando dim ker C > 0, anzi tale
situazione è la più frequente. dim ker C > 0 significa solo che non possiamo dedurre lo stato
mediante una trasformazione algebrica dell'uscita e questa, ripeto, è la situazione di gran lunga
più comune. Il fatto che E-(0,0) contenga stati diversi da zero significa invece che non è
possibile dedurre lo stato del sistema mediante un osservatore che, ricordiamolo bene, è un sistema
dinamico che ricostruisce (si dovrebbe, come vi ho detto più volte, chiamarlo ricostruttore) lo stato
in base ai valori assunti dall'uscita e dall'ingresso in un certo intervallo di tempo, non in un solo
istante.
Sbaglia nel legare il sottospazio di inosservabilità al nucleo della matrice di distribuzione delle uscite;
E-(0,0) può benissimo contenere il solo vettore 0 anche quando dim ker C > 0, anzi tale
situazione è la più frequente. dim ker C > 0 significa solo che non possiamo dedurre lo stato
mediante una trasformazione algebrica dell'uscita e questa, ripeto, è la situazione di gran lunga
più comune. Il fatto che E-(0,0) contenga stati diversi da zero significa invece che non è
possibile dedurre lo stato del sistema mediante un osservatore che, ricordiamolo bene, è un sistema
dinamico che ricostruisce (si dovrebbe, come vi ho detto più volte, chiamarlo ricostruttore) lo stato
in base ai valori assunti dall'uscita e dall'ingresso in un certo intervallo di tempo, non in un solo
istante.
 #92
Una retroazione sull'ingresso dello stato, stimato mediante un osservatore identità in un sistema dinamico,
lineare, stazionario, in forma minima, completamente raggiungibile, stabile ilsl, può portare a un sistema
non stabilizzabile ilsl, visto che può modificare ad arbitrio tutti gli autovalori del sistema (blocco
raggiungibile e osservabile)? (Wed Jan 5 10:50:40 2000, R.R.) #92
Una retroazione sull'ingresso dello stato, stimato mediante un osservatore identità in un sistema dinamico,
lineare, stazionario, in forma minima, completamente raggiungibile, stabile ilsl, può portare a un sistema
non stabilizzabile ilsl, visto che può modificare ad arbitrio tutti gli autovalori del sistema (blocco
raggiungibile e osservabile)? (Wed Jan 5 10:50:40 2000, R.R.)
 Il sistema in oggetto è completamente raggiungibile e tale caratteristica non può venire modificata da
una retroazione tra lo stato o lo stato osservato e l'ingresso (che non modifica né la dimensione né
l'orientamento del sottospazio di raggiungibilità, qui coincidente con l'intero spazio degli stati).
Ne segue che una retroazione del tipo considerato può rendere il sistema instabile ilsl (ma qui la
stabilità ilsl coincide con la ulsl e quella asintotica) ma non non stabilizzabile.
Il sistema in oggetto è completamente raggiungibile e tale caratteristica non può venire modificata da
una retroazione tra lo stato o lo stato osservato e l'ingresso (che non modifica né la dimensione né
l'orientamento del sottospazio di raggiungibilità, qui coincidente con l'intero spazio degli stati).
Ne segue che una retroazione del tipo considerato può rendere il sistema instabile ilsl (ma qui la
stabilità ilsl coincide con la ulsl e quella asintotica) ma non non stabilizzabile.
 #92
Perché la retroazione stato-ingresso non modifica la dimensione di R+(0)?
Vale la relazione R+(0)=im [B AB ... An-1B] =
im [B (A+BK)B ... (A+BK)n-1B] o i due spazi hanno solo
la stessa dimensione? (Tue Jan 4 18:38:56 2000, Alessandro Caselli) #92
Perché la retroazione stato-ingresso non modifica la dimensione di R+(0)?
Vale la relazione R+(0)=im [B AB ... An-1B] =
im [B (A+BK)B ... (A+BK)n-1B] o i due spazi hanno solo
la stessa dimensione? (Tue Jan 4 18:38:56 2000, Alessandro Caselli)
 La retroazione stato-ingresso non può diminuire la dimensione del sottospazio di
raggiungibilità perché, come può dedurre immediatamente dalle espressioni presenti
nella sua domanda, tutte le colonne della matrice di raggiungibilità del sistema
non retroazionato sono presenti anche in quella del sistema retroazionato.
Non può neppure aumentarne la dimensione perchè, agendo attraverso l'ingresso,
può modificare solo le caratteristiche della parte raggiungibile. Osservando la
struttura dei termini della matrice di raggiungibilità del sistema retroazionato
è poi facile dedurre la coincidenza dei due sottospazi (suggerimento per la
dimostrazione: si ricordi che R+(0)=mi(A,im B)).
La retroazione stato-ingresso non può diminuire la dimensione del sottospazio di
raggiungibilità perché, come può dedurre immediatamente dalle espressioni presenti
nella sua domanda, tutte le colonne della matrice di raggiungibilità del sistema
non retroazionato sono presenti anche in quella del sistema retroazionato.
Non può neppure aumentarne la dimensione perchè, agendo attraverso l'ingresso,
può modificare solo le caratteristiche della parte raggiungibile. Osservando la
struttura dei termini della matrice di raggiungibilità del sistema retroazionato
è poi facile dedurre la coincidenza dei due sottospazi (suggerimento per la
dimostrazione: si ricordi che R+(0)=mi(A,im B)).
 #93
Se la risposta libera, a partire da un opportuno stato iniziale, di un sistema dinamico, lineare, stazionario,
ha andamento sinusoidale, il sistema può essere asintoticamente stabile, se gli autovalori immaginari coniugati
hanno parte reale <0? (Wed Jan 5 10:50:40 2000, R.R.) #93
Se la risposta libera, a partire da un opportuno stato iniziale, di un sistema dinamico, lineare, stazionario,
ha andamento sinusoidale, il sistema può essere asintoticamente stabile, se gli autovalori immaginari coniugati
hanno parte reale <0? (Wed Jan 5 10:50:40 2000, R.R.)
 Se la sinusoide osservata è smorzata, ha cioè ampiezza che tende a zero al tendere del tempo all'infinito,
il sistema può essere asintoticamente stabile. Se invece l'ampiezza di tale sinusoide è costante o cresce
con il tempo il sistema non può risultare asintoticamente stabile. Se ne può rendere facilmente conto
riguardando l'andamento nel tempo dei modi del sistema.
Se la sinusoide osservata è smorzata, ha cioè ampiezza che tende a zero al tendere del tempo all'infinito,
il sistema può essere asintoticamente stabile. Se invece l'ampiezza di tale sinusoide è costante o cresce
con il tempo il sistema non può risultare asintoticamente stabile. Se ne può rendere facilmente conto
riguardando l'andamento nel tempo dei modi del sistema.
 #94
Relativamente all'esercizio 5 sui sistemi elettromeccanici, potrebbe spiegarmi come cambia il modello
nello spazio degli stati dell'altoparlante, quando questo è comandato in corrente anzichè in tensione?
(Fri Jan 7 10:58:01 2000, Gabriele Predoli) #94
Relativamente all'esercizio 5 sui sistemi elettromeccanici, potrebbe spiegarmi come cambia il modello
nello spazio degli stati dell'altoparlante, quando questo è comandato in corrente anzichè in tensione?
(Fri Jan 7 10:58:01 2000, Gabriele Predoli)
 La differenza è molto semplice. Quando pilotiamo (come si fa comunemente) un altoparlante
in tensione, la corrente che circola nella bobina mobile e quindi la forza che agisce
sulla stessa è governata dal circuito RL della bobina stessa e dalla forza controelettromotrice
indotta in tale circuito a causa del suo movimento in un campo
magnetico (può trovare la trattazione completa nell'esercizio 11 del testo Teoria
dei Sistemi: Esercizi e Applicazioni); il modello globale risultante è di ordine 3.
Se si collega la bobina mobile ad un generatore di corrente, la corrente che circola
nella bobina non dipende più nè dalla resistenza nè dalla induttanza del circuito e
neppure dalla forza controelettromotrice; il modello risultante diventa di ordine 2
dato che l'ingresso applicato equivale ad una forza applicata direttamente al cono.
La differenza è molto semplice. Quando pilotiamo (come si fa comunemente) un altoparlante
in tensione, la corrente che circola nella bobina mobile e quindi la forza che agisce
sulla stessa è governata dal circuito RL della bobina stessa e dalla forza controelettromotrice
indotta in tale circuito a causa del suo movimento in un campo
magnetico (può trovare la trattazione completa nell'esercizio 11 del testo Teoria
dei Sistemi: Esercizi e Applicazioni); il modello globale risultante è di ordine 3.
Se si collega la bobina mobile ad un generatore di corrente, la corrente che circola
nella bobina non dipende più nè dalla resistenza nè dalla induttanza del circuito e
neppure dalla forza controelettromotrice; il modello risultante diventa di ordine 2
dato che l'ingresso applicato equivale ad una forza applicata direttamente al cono.
 #95
Se due basi dei sottospazi E-(0,0) e R+(0) sono date
rispettivamente da #95
Se due basi dei sottospazi E-(0,0) e R+(0) sono date
rispettivamente da
| 1 0 | | 0 1 -6 36 |
| 0 0 | | 0 0 0 0 |
| 0 0 | | 0 1 -8 49 |
| 0 0 | | 1 -3 9 -27 |
| 0 1 | | 0 0 9 -47 |
quanto vale una base della intersezione di tali sottospazi (per determinare
una base della parte raggiungibile e osservabile nella scomposizione canonica di Kalman).
(Sun Jan 9 11:18:05 2000, R.R.)
 Utilizzando la modalità di calcolo che abbiamo visto sia a lezione che nelle esercitazioni
per il calcolo della intersezione di due sottospazi come complemento ortogonale della somma
dei due complementi ortogonali, si ricava immediatamente (il complemento ortogonale
di R+(0) ha come base la seconda colonna della identità, il complemento
ortogonale di E-(0,0) la seconda, terza e quarta colonna della identità)
che l'intersezione cercata coincide con E-(0,0) ed ha, quindi la stessa
base. Questo è un caso nel quale una operazione complicata (intersezione di due sottospazi)
non richiede alcun calcolo purché, naturalmente, si conosca con chiarezza il procedimento
da seguire. Spero anche non le sfugga che l'intersezione tra tali sottospazi descrive la
parte raggiungibile e non osservabile del sistema.
Utilizzando la modalità di calcolo che abbiamo visto sia a lezione che nelle esercitazioni
per il calcolo della intersezione di due sottospazi come complemento ortogonale della somma
dei due complementi ortogonali, si ricava immediatamente (il complemento ortogonale
di R+(0) ha come base la seconda colonna della identità, il complemento
ortogonale di E-(0,0) la seconda, terza e quarta colonna della identità)
che l'intersezione cercata coincide con E-(0,0) ed ha, quindi la stessa
base. Questo è un caso nel quale una operazione complicata (intersezione di due sottospazi)
non richiede alcun calcolo purché, naturalmente, si conosca con chiarezza il procedimento
da seguire. Spero anche non le sfugga che l'intersezione tra tali sottospazi descrive la
parte raggiungibile e non osservabile del sistema.
 #96
Dato un sistema lineare stazionario continuo, si richiede il modello della parte
raggiungibile del sistema. Non riesco a trovare la trasformazione di coordinate T;
mi sembra di capire che occorre R+(0)=imP e E-(0,0)=kerQ.
A tale proposito ho 3 domande: Quando arresto lo sviluppo di P=[B AB .. A(n-1)B] e di
Q? Se P e Q sono calcolate corrette, ho i sottospazi corrispondenti, come si calcola
l'intersezione di tali sottospazi? E dall'imT1 come ricavo la colonna T1?
(Tue Jan 11 23:33:45 2000, Enrico Macchiavelli) #96
Dato un sistema lineare stazionario continuo, si richiede il modello della parte
raggiungibile del sistema. Non riesco a trovare la trasformazione di coordinate T;
mi sembra di capire che occorre R+(0)=imP e E-(0,0)=kerQ.
A tale proposito ho 3 domande: Quando arresto lo sviluppo di P=[B AB .. A(n-1)B] e di
Q? Se P e Q sono calcolate corrette, ho i sottospazi corrispondenti, come si calcola
l'intersezione di tali sottospazi? E dall'imT1 come ricavo la colonna T1?
(Tue Jan 11 23:33:45 2000, Enrico Macchiavelli)
 La determinazione della sola parte raggiungibile di un sistema non richiede che si effettui
l'intera scomposizione canonica di Kalman del sistema; è sufficiente passare ad una base
partizionata in una base del sottospazio di raggiungibilità e in un insieme di vettori che
completino la base dell'intero spazio (riveda, a tale riguardo, quanto abbiamo visto a
lezione e quanto riportato al punto c) dell'esercizio 2 sul libro Teoria dei Sistemi:
Esercizi e applicazioni). Per quanto riguarda poi le domande specifiche che mi pone:
1) L'arresto dei termini presenti in P e Q viene operato non appena si incontra
una matrice le cui colonne risultino linearmente dipendenti dalle precedenti. 2) L'intersezione
di due sottospazi viene calcolata (anche questo lo abbiamo visto sia a lezione che nelle
esercitazioni) come complemento ortogonale della somma dei complementi ortogonali dei due
sottospazi. 3) La terza domanda non è formulata in maniera corretta: non vi è infatti alcun
motivo perché, in generale, la sottomatrice T1 debba essere formata da
una sola colonna (tale sottomatrice può avere da 0 ad n colonne). Se la domanda
riguarda le modalità di calcolo di una base per lo spazio generato dalle colonne di
una matrice, allora la risposta può essere: mediante l'algoritmo di ortonormalizzazione
di Gram-Schmidt. Penso le possa tornare utile studiare a fondo l'intero esercizio 2
citato poco sopra.
La determinazione della sola parte raggiungibile di un sistema non richiede che si effettui
l'intera scomposizione canonica di Kalman del sistema; è sufficiente passare ad una base
partizionata in una base del sottospazio di raggiungibilità e in un insieme di vettori che
completino la base dell'intero spazio (riveda, a tale riguardo, quanto abbiamo visto a
lezione e quanto riportato al punto c) dell'esercizio 2 sul libro Teoria dei Sistemi:
Esercizi e applicazioni). Per quanto riguarda poi le domande specifiche che mi pone:
1) L'arresto dei termini presenti in P e Q viene operato non appena si incontra
una matrice le cui colonne risultino linearmente dipendenti dalle precedenti. 2) L'intersezione
di due sottospazi viene calcolata (anche questo lo abbiamo visto sia a lezione che nelle
esercitazioni) come complemento ortogonale della somma dei complementi ortogonali dei due
sottospazi. 3) La terza domanda non è formulata in maniera corretta: non vi è infatti alcun
motivo perché, in generale, la sottomatrice T1 debba essere formata da
una sola colonna (tale sottomatrice può avere da 0 ad n colonne). Se la domanda
riguarda le modalità di calcolo di una base per lo spazio generato dalle colonne di
una matrice, allora la risposta può essere: mediante l'algoritmo di ortonormalizzazione
di Gram-Schmidt. Penso le possa tornare utile studiare a fondo l'intero esercizio 2
citato poco sopra.
 #97
Nei miei appunti, alla fine della Raggiungibilità e Controllabilità per i sistemi lineari
non stazionari continui ho scritto che R+ ed R- hanno la stessa
dimensione. E' corretto?
Se è corretto lo si può anche completare affermando che i due sottospazi coincidono
quindi "se tale sistema è completamente raggiungibile ==> è anche completamente
controllabile" e viceversa? (Mon Jan 17 15:59:26 2000, Claudio Beltrani) #97
Nei miei appunti, alla fine della Raggiungibilità e Controllabilità per i sistemi lineari
non stazionari continui ho scritto che R+ ed R- hanno la stessa
dimensione. E' corretto?
Se è corretto lo si può anche completare affermando che i due sottospazi coincidono
quindi "se tale sistema è completamente raggiungibile ==> è anche completamente
controllabile" e viceversa? (Mon Jan 17 15:59:26 2000, Claudio Beltrani)
 L'eguaglianza delle dimensioni dei due sottospazi deriva dalla non singolarità della
matrice di transizione della classe di sistemi considerata che, a sua volta, non
implica, per i sistemi lineari non stazionari, l'eguaglianza dei due sottospazi.
Nel caso uno dei due sottospazi coincida con l'intero spazio, ne segue, ovviamente,
che anche l'altro sottospazio coinciderà con l'intero spazio.
L'eguaglianza delle dimensioni dei due sottospazi deriva dalla non singolarità della
matrice di transizione della classe di sistemi considerata che, a sua volta, non
implica, per i sistemi lineari non stazionari, l'eguaglianza dei due sottospazi.
Nel caso uno dei due sottospazi coincida con l'intero spazio, ne segue, ovviamente,
che anche l'altro sottospazio coinciderà con l'intero spazio.
 #98
Sempre nei miei appunti, all'inizio dell'Osservabilità e Ricostruibilità dei sistemi
lineari non stazionari continui ho scritto che un sistema lineare non stazionario
continuo che risulti diagnosticabile lo è anche completamente (cioè è diagnosticabile
indipendentemente dall'ingresso applicato). E' corretto?
(Mon Jan 17 15:59:26 2000, Claudio Beltrani) #98
Sempre nei miei appunti, all'inizio dell'Osservabilità e Ricostruibilità dei sistemi
lineari non stazionari continui ho scritto che un sistema lineare non stazionario
continuo che risulti diagnosticabile lo è anche completamente (cioè è diagnosticabile
indipendentemente dall'ingresso applicato). E' corretto?
(Mon Jan 17 15:59:26 2000, Claudio Beltrani)
 Sì, grazie alla scomposizione della risposta in risposta libera e risposta forzata.
Sì, grazie alla scomposizione della risposta in risposta libera e risposta forzata.
 #99
Il viceversa della Proprietà C3.1.4 a pag. 92 del libro di testo vale per ogni tipo di
sistema? Anche per i non lineari stazionari e non stazionari?
(Mon Jan 17 15:59:26 2000, Claudio Beltrani) #99
Il viceversa della Proprietà C3.1.4 a pag. 92 del libro di testo vale per ogni tipo di
sistema? Anche per i non lineari stazionari e non stazionari?
(Mon Jan 17 15:59:26 2000, Claudio Beltrani)
 La proprietà indicata (completa osservabilità e ricostruibilità) vale solo
per i sistemi lineari grazie alla proprietà di scomposizione della risposta.
Può facilmente convincersi di questo pensando al problema della diagnosi
e dell'incasellamento per i sistemi a stati finiti.
La proprietà indicata (completa osservabilità e ricostruibilità) vale solo
per i sistemi lineari grazie alla proprietà di scomposizione della risposta.
Può facilmente convincersi di questo pensando al problema della diagnosi
e dell'incasellamento per i sistemi a stati finiti.
 #100
Se lo stato iniziale x dà uscita y(.) con ingresso u(.) nell'intervallo
[t0,t1],
tutti gli altri stati iniziali che danno uscita y(.) fanno parte di: #100
Se lo stato iniziale x dà uscita y(.) con ingresso u(.) nell'intervallo
[t0,t1],
tutti gli altri stati iniziali che danno uscita y(.) fanno parte di:
a) E-(t0,t1,0,0)?
b) E-(t0,t1,0,y(.))?
c) E-(t0,t1,0,y0(.))?
d) alcuni possono fare parte di
E-(t0,t1,u(.),y0(.))?
(Mon Jan 17 15:59:26 2000, Claudio Beltrani)
 Se il sistema considerato è lineare (lei non lo specifica), l'insieme di stati iniziali che,
con l'ingresso u(.) danno l'uscita y(.) in
[t0,t1] è la varietà lineare definita da
E-(t0,t1,u(.),y(.)) e
dal sottospazio E-(t0,t1,0,0).
Se il sistema considerato è lineare (lei non lo specifica), l'insieme di stati iniziali che,
con l'ingresso u(.) danno l'uscita y(.) in
[t0,t1] è la varietà lineare definita da
E-(t0,t1,u(.),y(.)) e
dal sottospazio E-(t0,t1,0,0).
 #101
Un sistema in forma minima è sempre completamente osservabile , o ciò è vero se e solo
se il sistema è lineare? (Mon Jan 17 15:59:26 2000, Claudio Beltrani) #101
Un sistema in forma minima è sempre completamente osservabile , o ciò è vero se e solo
se il sistema è lineare? (Mon Jan 17 15:59:26 2000, Claudio Beltrani)
 Solo se è lineare, per i motivi più volte riportati nelle domande precedenti.
Solo se è lineare, per i motivi più volte riportati nelle domande precedenti.
 #102
Un sistema lineare continuo completamente ricostruibile è
anche completamente osservabile (vedi Proprietà C3.1.3 a pag. 92 libro di testo).
Non è necessario che sia anche in forma minima? Perchè tale proprietà non vale anche per
i sistemi discreti? (Mon Jan 17 15:59:26 2000, Claudio Beltrani) #102
Un sistema lineare continuo completamente ricostruibile è
anche completamente osservabile (vedi Proprietà C3.1.3 a pag. 92 libro di testo).
Non è necessario che sia anche in forma minima? Perchè tale proprietà non vale anche per
i sistemi discreti? (Mon Jan 17 15:59:26 2000, Claudio Beltrani)
 La completa ricostruibilità implica che nell'insieme degli stati non esistano stati
equivalenti quindi che il sistema sia in forma minima. Un sistema discreto può
risultare completamente ricostruibile ma non completamente osservabile a causa
della possibile singolarità della matrice di transizione (riveda l'esempio che
ho fatto, a tale riguardo, a lezione); naturalmente per i modelli discreti
dei sistemi continui valgono le stesse proprietà dei sistemi continui dato che
la loro matrice di transizione è sempre non singolare.
La completa ricostruibilità implica che nell'insieme degli stati non esistano stati
equivalenti quindi che il sistema sia in forma minima. Un sistema discreto può
risultare completamente ricostruibile ma non completamente osservabile a causa
della possibile singolarità della matrice di transizione (riveda l'esempio che
ho fatto, a tale riguardo, a lezione); naturalmente per i modelli discreti
dei sistemi continui valgono le stesse proprietà dei sistemi continui dato che
la loro matrice di transizione è sempre non singolare.
 #103
A pag. 95 del libro di testo si ha che F(A)=sommatoria da 0 a
(m-1) delle potenze di A, con m grado del polinomio minimo.
Supponendo che A sia una n x n
e m < n avrò solo m modi , quindi la matrice di transizione sarà data solo
dalla somma di m potenze (avrò solo m coefficenti gamma).
La matrice di transizione sarà sempre una n x n?
(Mon Jan 17 15:59:26 2000, Claudio Beltrani) #103
A pag. 95 del libro di testo si ha che F(A)=sommatoria da 0 a
(m-1) delle potenze di A, con m grado del polinomio minimo.
Supponendo che A sia una n x n
e m < n avrò solo m modi , quindi la matrice di transizione sarà data solo
dalla somma di m potenze (avrò solo m coefficenti gamma).
La matrice di transizione sarà sempre una n x n?
(Mon Jan 17 15:59:26 2000, Claudio Beltrani)
 Certamente come, d'altronde, qualunque altra funzione di A. Questa è una
conseguenza immediata della definizione di funzione di matrice.
Certamente come, d'altronde, qualunque altra funzione di A. Questa è una
conseguenza immediata della definizione di funzione di matrice.
 #103
In relazione alla secondo test presente nell'area Autovalutazione, vorrei
sapere perché la risposta 3 è corretta (la domanda è stata riassunta dato che il test
è accessibile sul server)
(Tue Jan 18 16:13:46 2000, Luca Scalorbi) #103
In relazione alla secondo test presente nell'area Autovalutazione, vorrei
sapere perché la risposta 3 è corretta (la domanda è stata riassunta dato che il test
è accessibile sul server)
(Tue Jan 18 16:13:46 2000, Luca Scalorbi)
 La linearità del sistema determina la additività del contributo dell'ingresso
alla risposta libera dei due stati; qualunque altro ingresso modificherà
quindi nella stessa misura le risposte libere di tali stati che risultano,
di conseguenza, indistinguibili nell'intervallo considerato.
La linearità del sistema determina la additività del contributo dell'ingresso
alla risposta libera dei due stati; qualunque altro ingresso modificherà
quindi nella stessa misura le risposte libere di tali stati che risultano,
di conseguenza, indistinguibili nell'intervallo considerato.
 #104
Ad un certo punto dei miei appunti viene affermato che:
BTeAT(t1- #104
Ad un certo punto dei miei appunti viene affermato che:
BTeAT(t1-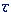 )x1
= BTeAT )x1
= BTeAT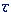 x1 con x1 con
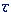 compreso tra 0 e t1. Perché?
(Sun Jan 23 15:26:03 2000, Danilo Tardioli) compreso tra 0 e t1. Perché?
(Sun Jan 23 15:26:03 2000, Danilo Tardioli)
 I suoi appunti non sono completi; la proprietà che abbiamo utilizzato è infatti la seguente:
BTeAT(t1-
I suoi appunti non sono completi; la proprietà che abbiamo utilizzato è infatti la seguente:
BTeAT(t1-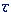 )x1=0
per )x1=0
per 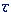 compreso tra 0 e t1 equivale alla condizione
BTeAT compreso tra 0 e t1 equivale alla condizione
BTeAT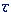 x1=0
sempre per x1=0
sempre per 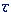 compreso tra 0 e t1 e questa
proprietà è di verifica immediata. compreso tra 0 e t1 e questa
proprietà è di verifica immediata.
 #105
Ho poi scritto che BTeAT #105
Ho poi scritto che BTeAT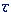 x1
è una funzione analitica (che significa?) e che condizione necessaria e sufficiente affinché tale
funzione si annulli per qualunque x1
è una funzione analitica (che significa?) e che condizione necessaria e sufficiente affinché tale
funzione si annulli per qualunque 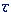 compreso tra 0 e t1
è che si annullino anche tutte le sue derivate in [0,t1]. Perché?
(Sun Jan 23 15:26:03 2000, Danilo Tardioli) compreso tra 0 e t1
è che si annullino anche tutte le sue derivate in [0,t1]. Perché?
(Sun Jan 23 15:26:03 2000, Danilo Tardioli)
 Una funzione analitica in un certo intervallo è una funzione continua che ammette derivate continue
di qualunque ordine. Condizione necessaria e sufficiente perché una funzione analitica si
annulli in tutti i punti di un intervallo è che si annulli, assieme a tutte le sue derivate,
in un punto (arbitrario) di tale intervallo. Nella dimostrazione cui lei fa riferimento
abbiamo considerato, per semplicità, il punto
Una funzione analitica in un certo intervallo è una funzione continua che ammette derivate continue
di qualunque ordine. Condizione necessaria e sufficiente perché una funzione analitica si
annulli in tutti i punti di un intervallo è che si annulli, assieme a tutte le sue derivate,
in un punto (arbitrario) di tale intervallo. Nella dimostrazione cui lei fa riferimento
abbiamo considerato, per semplicità, il punto 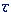 =0. =0.
 #106
In riferimento al tema d'esame numero 2 dei sistemi meccanici elettromeccanici ed elettrici:
a me risulta un funzione di trasferimento nulla, è possibile? (Tue Jan 25 08:34:40 2000, Matteo Tiraferri) #106
In riferimento al tema d'esame numero 2 dei sistemi meccanici elettromeccanici ed elettrici:
a me risulta un funzione di trasferimento nulla, è possibile? (Tue Jan 25 08:34:40 2000, Matteo Tiraferri)
 No, dato che la tensione applicata alla bobina genera una corrente e, conseguentemente, una forza
che agisce sulla bobina stessa (che si trova immersa in un campo magnetico). Tale forza determina
uno spostamento tale che il richiamo elastico la bilanci esattamente.
No, dato che la tensione applicata alla bobina genera una corrente e, conseguentemente, una forza
che agisce sulla bobina stessa (che si trova immersa in un campo magnetico). Tale forza determina
uno spostamento tale che il richiamo elastico la bilanci esattamente.
 #107
Con riferimento al testo d'esame 6 della sezione "Sistemi lineari (modello assegnato)",
come si calcola uno stato equivalente in un sistema lineare? (Tue Jan 25 08:49:36 2000, Matteo Tiraferri) #107
Con riferimento al testo d'esame 6 della sezione "Sistemi lineari (modello assegnato)",
come si calcola uno stato equivalente in un sistema lineare? (Tue Jan 25 08:49:36 2000, Matteo Tiraferri)
 Dato uno stato, x, di un sistema lineare, tutti (e soli) gli stati equivalenti si ottengono
sommando ad x gli stati del sottospazio di inosservabilità E-(0,0).
Dato uno stato, x, di un sistema lineare, tutti (e soli) gli stati equivalenti si ottengono
sommando ad x gli stati del sottospazio di inosservabilità E-(0,0).
 #108
Sia S un sistema dinamico, lineare e stazionario, a dimensioni infinite il cui
ingresso e la cui uscita appartengono a spazi vettoriali a dimensioni finite.
Perché non è possibile rappresentare tale sistema con un modello polinomiale di
ingresso-uscita? Quale tipo di sistema è descrivibile da un modello polinomiale
di ingresso-uscita? (Thu Jan 27 14:56:38 2000, G.X.) #108
Sia S un sistema dinamico, lineare e stazionario, a dimensioni infinite il cui
ingresso e la cui uscita appartengono a spazi vettoriali a dimensioni finite.
Perché non è possibile rappresentare tale sistema con un modello polinomiale di
ingresso-uscita? Quale tipo di sistema è descrivibile da un modello polinomiale
di ingresso-uscita? (Thu Jan 27 14:56:38 2000, G.X.)
 I modelli polinomiali di ingresso-uscita (con polinomi a coefficienti costanti) non sono in grado
di descrivere la dinamica interna di eventuali parti osservabili ma non raggiungibili di un sistema
a parametri distribuiti; potrebbero svolgere questo ruolo solo considerando coefficienti in grado
di assumere valori locali. Il problema non si pone per la funzione di trasferimento o la risposta
impulsiva a causa delle dimensioni finite ipotizzate per i relativi spazi vettoriali. Tali modelli
descrivono sistemi lineari stazionari completamente osservabili e con spazio degli stati a
dimensioni finite.
I modelli polinomiali di ingresso-uscita (con polinomi a coefficienti costanti) non sono in grado
di descrivere la dinamica interna di eventuali parti osservabili ma non raggiungibili di un sistema
a parametri distribuiti; potrebbero svolgere questo ruolo solo considerando coefficienti in grado
di assumere valori locali. Il problema non si pone per la funzione di trasferimento o la risposta
impulsiva a causa delle dimensioni finite ipotizzate per i relativi spazi vettoriali. Tali modelli
descrivono sistemi lineari stazionari completamente osservabili e con spazio degli stati a
dimensioni finite.
 #109
Quand'è che si semplificano dei fattori nel passaggio dal modello ISU alla G(s) e che perdita di informazione
si verifica (in particolare in termini di descrizione delle diverse parti della scomposizione di Kalman)?
(Sun May 21 11:23:29 2000, Andrea Di Vincenzo) #109
Quand'è che si semplificano dei fattori nel passaggio dal modello ISU alla G(s) e che perdita di informazione
si verifica (in particolare in termini di descrizione delle diverse parti della scomposizione di Kalman)?
(Sun May 21 11:23:29 2000, Andrea Di Vincenzo)
 Nella eliminazione del massimo comun divisore sinistro di P(s) e Q(s);
se P(s)=M(s)P'(s) e Q(s)=M(s)Q'(s), G(s)=Q(s)-1P(s)=Q'(s)-1P'(s).
La parte non rappresentata dalla G(s) è quella osservabile ma non raggiungibile.
Nella eliminazione del massimo comun divisore sinistro di P(s) e Q(s);
se P(s)=M(s)P'(s) e Q(s)=M(s)Q'(s), G(s)=Q(s)-1P(s)=Q'(s)-1P'(s).
La parte non rappresentata dalla G(s) è quella osservabile ma non raggiungibile.
 #110
Considerato un sistema discreto la sua matrice di transizione non è in generale invertibile.
Dunque in quel caso la completa controllabilità non è implicata in generale dalla completa
raggiungibilità (giusto?). Però se immagino un sistema a stati finiti (che pure è discreto)
completamente raggiungibile, cioè tale che ogni stato sia raggiungibile da tutti gli altri,
non mi pare possibile che esistano casi in cui contemporaneamente non sia anche completamente
controllabile. (Andrea Di Vincenzo, Tue May 23 17:13:24 2000) #110
Considerato un sistema discreto la sua matrice di transizione non è in generale invertibile.
Dunque in quel caso la completa controllabilità non è implicata in generale dalla completa
raggiungibilità (giusto?). Però se immagino un sistema a stati finiti (che pure è discreto)
completamente raggiungibile, cioè tale che ogni stato sia raggiungibile da tutti gli altri,
non mi pare possibile che esistano casi in cui contemporaneamente non sia anche completamente
controllabile. (Andrea Di Vincenzo, Tue May 23 17:13:24 2000)
 Sbagliato. È la completa raggiungibilità che non è implicata dalla completa controllabilità
come può dedurre anche dagli esempi fatti a lezione. I paragoni poi tra i sistemi a stati
finiti (non lineari) ed i sistemi a stato vettore lineari a tempo discreto sono del tutto
fuori luogo dato che tali classi di sistemi hanno proprietà molto diverse.
Sbagliato. È la completa raggiungibilità che non è implicata dalla completa controllabilità
come può dedurre anche dagli esempi fatti a lezione. I paragoni poi tra i sistemi a stati
finiti (non lineari) ed i sistemi a stato vettore lineari a tempo discreto sono del tutto
fuori luogo dato che tali classi di sistemi hanno proprietà molto diverse.
| 

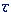 )x1
= BTeAT
)x1
= BTeAT